Trigonometry
- A vertical pole AB is standing at the centre B of a square PQRS.If PR subtends an angle of 90° at the top, A of the pole, then the angle subtended by a side of the square at A is :
-
View Hint View Answer Discuss in Forum
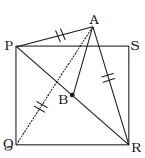
PA = PR
∠APB = ∠ARB = 45°
If PR = √2x :PB = x √2
From triangle APB ,tan45° = AB ⇒ AB = PB = x PB √2
∴ PA = √( x2 / 2 ) + ( x2 / 2 ) = √x2 = x
∴ QA = PQ = PA = x
∴ ∠PAQ = 60°Correct Option: C

PA = PR
∠APB = ∠ARB = 45°
If PR = √2x :PB = x √2
From triangle APB ,tan45° = AB ⇒ AB = PB = x PB √2
∴ PA = √( x2 / 2 ) + ( x2 / 2 ) = √x2 = x
∴ QA = PQ = PA = x
∴ ∠PAQ = 60°
-
For how many integral values of ‘x’, sin φ = ( 3x - 2) , where
0° ⋜ φ ⋜ 90°4
-
View Hint View Answer Discuss in Forum
0° ⋜ φ ⋜ 90°
∴ 0 ⋜ sin φ ⋜ 1∵ sin φ = 3x - 2 4 When , x = 1 , sin φ = 1 4 When , x = 2 , sin φ = 4 = 1 4 Correct Option: A
0° ⋜ φ ⋜ 90°
∴ 0 ⋜ sin φ ⋜ 1∵ sin φ = 3x - 2 4 When , x = 1 , sin φ = 1 4 When , x = 2 , sin φ = 4 = 1 4
-
Find the value of cot π - tan π - 2tan π 32 32 16
-
View Hint View Answer Discuss in Forum
cot π - tan π - 2tan π 32 32 16 = cos(π / 32) - sin(π / 32) - 2tan π sin(π / 32) cos(π / 32) 16 = cos2(π / 32) - sin2(π / 32) - 2tan π sin(π / 32) × cos(π / 32) 16 = 2cos(π / 16) - 2tan π 2sin(π / 32).cos(π / 32) 16
{ ∴ cos2θ - sin2θ = cos2θ }= 2cos(π / 16) - 2tan π sin(π / 16) 16
{∴ sin 2θ = 2sinθ . cosθ }= 2 
cos(π / 16) - sin( π/ 16 ) 
sin(π / 16) cos(π / 16) = 2 
cos2(π / 16) - sin2( π/ 16 ) 
sin(π / 16) . cos(π / 16) = 4cos(π / 8) = 4cot π sin(π / 8) 8
Correct Option: A
cot π - tan π - 2tan π 32 32 16 = cos(π / 32) - sin(π / 32) - 2tan π sin(π / 32) cos(π / 32) 16 = cos2(π / 32) - sin2(π / 32) - 2tan π sin(π / 32) × cos(π / 32) 16 = 2cos(π / 16) - 2tan π 2sin(π / 32).cos(π / 32) 16
{ ∴ cos2θ - sin2θ = cos2θ }= 2cos(π / 16) - 2tan π sin(π / 16) 16
{∴ sin 2θ = 2sinθ . cosθ }= 2 
cos(π / 16) - sin( π/ 16 ) 
sin(π / 16) cos(π / 16) = 2 
cos2(π / 16) - sin2( π/ 16 ) 
sin(π / 16) . cos(π / 16) = 4cos(π / 8) = 4cot π sin(π / 8) 8
- If sin θ = a cos φ and cos θ = b sin φ , then the value of (a2 – 1) cot2 φ + (1 – b2 ) cot2θ is equal to :
-
View Hint View Answer Discuss in Forum
(a2 - 1)cot2φ + ( 1 - b2 )cot2 θ
= (a2 - 1) cos2φ + ( 1 - b2 ) cos2θ sin2φ sin2θ = (a2 - 1)cos2φ.sin2θ + ( 1 - b2 )cos2θ.sin2φ sin2φ.sin2θ = a2cos2φ.sin2θ - cos2φ.sin2θ + cos2θ.sin2φ - b2cos2θ.sin2φ sin2φ.sin2θ = sin2θ.sin2θ - cos2φ.sin2θ + cos2θ.sin2φ - cos2θ.cos2θ sin2φ.sin2θ
[ ∵ sinθ = bcosφ , cosθ = bsinφ ]= sin4θ - cos4θ - cos2φ.sin2θ + cos2θ.sin2φ sin2φ.sin2θ = (sin2θ - cos2θ)(sin2θ + cos2θ) - cos2φ.sin2θ + cos2θ.sin2φ sin2φ.sin2θ = sin2θ - cos2φ.sin2θ - cos2θ + cos2θ.sin2φ sin2φ.sin2θ = sin2θ( 1 - cos2φ ) - cos2θ( 1 - sin2φ ) sin2φ.sin2θ = sin2θ.sin2φ - cos2θ.cos2φ sin2φ.sin2θ = 1 - cos2θ.cos2φ = 1 - b2 sin2φ.sin2θ a2 Required answer = a2 - b2 a2
Correct Option: D
(a2 - 1)cot2φ + ( 1 - b2 )cot2 θ
= (a2 - 1) cos2φ + ( 1 - b2 ) cos2θ sin2φ sin2θ = (a2 - 1)cos2φ.sin2θ + ( 1 - b2 )cos2θ.sin2φ sin2φ.sin2θ = a2cos2φ.sin2θ - cos2φ.sin2θ + cos2θ.sin2φ - b2cos2θ.sin2φ sin2φ.sin2θ = sin2θ.sin2θ - cos2φ.sin2θ + cos2θ.sin2φ - cos2θ.cos2θ sin2φ.sin2θ
[ ∵ sinθ = bcosφ , cosθ = bsinφ ]= sin4θ - cos4θ - cos2φ.sin2θ + cos2θ.sin2φ sin2φ.sin2θ = (sin2θ - cos2θ)(sin2θ + cos2θ) - cos2φ.sin2θ + cos2θ.sin2φ sin2φ.sin2θ = sin2θ - cos2φ.sin2θ - cos2θ + cos2θ.sin2φ sin2φ.sin2θ = sin2θ( 1 - cos2φ ) - cos2θ( 1 - sin2φ ) sin2φ.sin2θ = sin2θ.sin2φ - cos2θ.cos2φ sin2φ.sin2θ = 1 - cos2θ.cos2φ = 1 - b2 sin2φ.sin2θ a2 Required answer = a2 - b2 a2
- If sec2θ + tan2θ = √3 , then the value of (sec4θ - tan4θ) is
-
View Hint View Answer Discuss in Forum
sec2θ + tan2θ = √3
and sec2θ - tan2θ = 1
∴ sec4θ - tan4θ = (sec2θ + tan2θ)(sec2θ - tan2θ)
sec4θ - tan4θ = √3 × 1 = √3Correct Option: C
sec2θ + tan2θ = √3
and sec2θ - tan2θ = 1
∴ sec4θ - tan4θ = (sec2θ + tan2θ)(sec2θ - tan2θ)
sec4θ - tan4θ = √3 × 1 = √3

