Trigonometry
- If θ is a positive acute angle and tan 2θ tan 3θ = 1, then the value of [2 cos² (5θ / 2) – 1[ is
-
View Hint View Answer Discuss in Forum
tan2θ . tan3θ = 1
⇒ tan 3θ = 1 = cot 2θ tan 2θ
⇒ tan3θ = tan (90° – 2θ )
⇒ 3θ = 90° – 2θ ⇒ 5θ = 90°
⇒ θ = 18∴ 2cos ² 5θ - 1 = 2 cos² 45° - 1 2
Correct Option: C
tan2θ . tan3θ = 1
⇒ tan 3θ = 1 = cot 2θ tan 2θ
⇒ tan3θ = tan (90° – 2θ )
⇒ 3θ = 90° – 2θ ⇒ 5θ = 90°
⇒ θ = 18∴ 2cos ² 5θ - 1 = 2 cos² 45° - 1 2
- If cos²α + cos²β = 2, then the value of tan&3 α+ sin5 β is :
-
View Hint View Answer Discuss in Forum
cos²α + cos²β = 2
⇒ 1 – sin²α + 1 – sin²β = 2
⇒ sin²α + sin²β = 0
⇒ sin²α = 0 & sin²β = 0
⇒ sinα = sinβ = 0
⇒ α = β = 0
∴ tan3α + sin5β = 0Correct Option: B
cos²α + cos²β = 2
⇒ 1 – sin²α + 1 – sin²β = 2
⇒ sin²α + sin²β = 0
⇒ sin²α = 0 & sin²β = 0
⇒ sinα = sinβ = 0
⇒ α = β = 0
∴ tan3α + sin5β = 0
- If tan2θ . tan 4θ = 1, then the value of tan 3θis
-
View Hint View Answer Discuss in Forum
tan 2θ = 1 = cot 4θ tan 4θ
⇒ tan 2θ = tan (90° – 4θ)
⇒ 2θ = 90° – 4θ
⇒ 6θ = 90° ⇒ θ = 15°
∴ tan 3θ = tan 45° = 1Correct Option: C
tan 2θ = 1 = cot 4θ tan 4θ
⇒ tan 2θ = tan (90° – 4θ)
⇒ 2θ = 90° – 4θ
⇒ 6θ = 90° ⇒ θ = 15°
∴ tan 3θ = tan 45° = 1
- If sinθ + cosecθ = 2, then the value of sin5θ +cosec5θ when 0° ≤ θ ≤ 90°, is
-
View Hint View Answer Discuss in Forum
sinθ + cosecθ = 2
sinθ = 1 = 2 sinθ
⇒ sin² θ - 2sin θ + 1 = 0
⇒ (sin θ - 1)² = 0 ⇒ sin θ = 1
∴ sin5θ + cosec5θ = 1 + 1 = 2Correct Option: D
sinθ + cosecθ = 2
sinθ = 1 = 2 sinθ
⇒ sin² θ - 2sin θ + 1 = 0
⇒ (sin θ - 1)² = 0 ⇒ sin θ = 1
∴ sin5θ + cosec5θ = 1 + 1 = 2
- If A = sin² θ + cos4θ, for any value of θ, then the value of A is
-
View Hint View Answer Discuss in Forum
When θ = 0°
sin2θ + cos4θ = 1
When θ = 45°,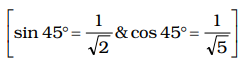
sin²θ + cos4θ = 1 + 1 = 3 2 4 4
when θ = 30°,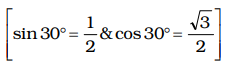
sin²θ + cos4θ = 1 + 9 4 16 = 4 + 9 = 13 16 16
Hence, the value ofA = sin2θ + cos4θ = 13 16
Correct Option: B
When θ = 0°
sin2θ + cos4θ = 1
When θ = 45°,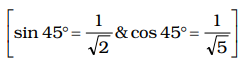
sin²θ + cos4θ = 1 + 1 = 3 2 4 4
when θ = 30°,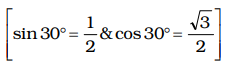
sin²θ + cos4θ = 1 + 9 4 16 = 4 + 9 = 13 16 16
Hence, the value ofA = sin2θ + cos4θ = 13 16

