441. The angle of elevation of the top of a tower from a point on the ground is 30° and moving 70 metres towards the tower it becomes 60°. The height of the tower is

1. 1. 10 metre

   
   
   

   2. 	10	metre
      	√3

   
   
   

   3. 10 √3 metre

   
   
   

   4. 35 √3 metre

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
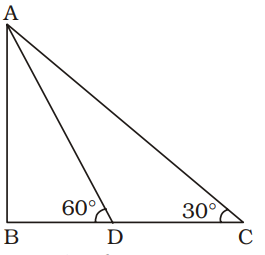
   AB = Height of tower = h metre (let)
   CD = 70 metre
   BD = x metre (let)
   In ∆ABC,
   

   tan30° =	AB
   	BC

   
   

   =	1	=	h
   	√3		x + 70

   
   ⇒ √3h = x + 70
   ⇒ x = √3h – 70 ............(i)
   In ∆ABD,
   

   tan60° =	h
   	x

   
   

   ⇒ √3 =	h
   	x

   
   

   ⇒ x =	h	.........(ii)
   	√3

   
   From equations (i) and (ii),
   

   ⇒ √3 - 70 =	h
   	√3

   
   

   ⇒ √3h -	h	= 70
   	√3

   
   

   =	3h - h	= 70
   	√3

   
   ⇒ 2h = 70 √3
   

   ⇒ h =	70√3	= 35 √3 metre
   	2

   Correct Option: D

   
   AB = Height of tower = h metre (let)
   CD = 70 metre
   BD = x metre (let)
   In ∆ABC,
   

   tan30° =	AB
   	BC

   
   

   =	1	=	h
   	√3		x + 70

   
   ⇒ √3h = x + 70
   ⇒ x = √3h – 70 ............(i)
   In ∆ABD,
   

   tan60° =	h
   	x

   
   

   ⇒ √3 =	h
   	x

   
   

   ⇒ x =	h	.........(ii)
   	√3

   
   From equations (i) and (ii),
   

   ⇒ √3 - 70 =	h
   	√3

   
   

   ⇒ √3h -	h	= 70
   	√3

   
   

   =	3h - h	= 70
   	√3

   
   ⇒ 2h = 70 √3
   

   ⇒ h =	70√3	= 35 √3 metre
   	2

---

442. If a pole of 12 m height casts a shadow of 4 √3 m long on the ground, then the sun’s angle of elevation at that instant is

1. 1. 30°

   
   
   

   2. 60°

   
   
   

   3. 45°

   
   
   

   4. 90° 16 cm is

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
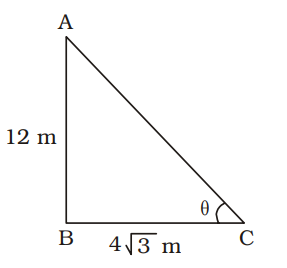
   AB = pole = 12 metre
   Shadow = BC = 4 √3 metre
   From ∆ABC,
   

   tanθ =	AB
   	BC

   
   

   =	12	= √3
   	4√3

   
   ⇒ tanθ = tan 60°
   ⇒ θ = 60°

   Correct Option: B

   
   AB = pole = 12 metre
   Shadow = BC = 4 √3 metre
   From ∆ABC,
   

   tanθ =	AB
   	BC

   
   

   =	12	= √3
   	4√3

   
   ⇒ tanθ = tan 60°
   ⇒ θ = 60°

---

---

443. The length of the shadow of a vertical tower on level ground increases by 10 metres when the altitude of the sun changes from 45° to 30°. Then the height of the tower is

1. 1. 5 ( √3 + 1) metres

   
   
   

   2. 5 ( √3 – 1) metres

   
   
   

   3. 5 √3 metres

   
   
   

   4. 	5	metres
      	√3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
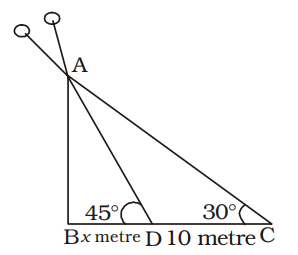
   AB = Tower = h metre
   BD = Shadow = x metre
   ∠ ADB = 45°
   ∠ ACB = 30°
   In ∆ ABD,
   

   tan 45° =	AB
   	BD

   
   

   ⇒ 1 =	h	⇒ h = x ..........(i)
   	x

   
   In ∆ ABC
   

   tan 30° =	AB
   	BC

   
   

   ⇒	1	=	h
   	√3		x + 10

   
   

   ⇒	1	=	h
   	√3		h + 10

   
   ⇒ √3 h = h + 10
   ⇒ √3 h – h = 10
   ⇒ h ( √3 –1) = 10
   

   ⇒ h =	10
   	√3 - 1

   
   

   =	10	×	√3 + 1
   	√3 - 1		√3 + 1

   
   

   =	10(√3 + 1)	= 5(√3 + 1) metre
   	3 - 1

   Correct Option: A

   
   AB = Tower = h metre
   BD = Shadow = x metre
   ∠ ADB = 45°
   ∠ ACB = 30°
   In ∆ ABD,
   

   tan 45° =	AB
   	BD

   
   

   ⇒ 1 =	h	⇒ h = x ..........(i)
   	x

   
   In ∆ ABC
   

   tan 30° =	AB
   	BC

   
   

   ⇒	1	=	h
   	√3		x + 10

   
   

   ⇒	1	=	h
   	√3		h + 10

   
   ⇒ √3 h = h + 10
   ⇒ √3 h – h = 10
   ⇒ h ( √3 –1) = 10
   

   ⇒ h =	10
   	√3 - 1

   
   

   =	10	×	√3 + 1
   	√3 - 1		√3 + 1

   
   

   =	10(√3 + 1)	= 5(√3 + 1) metre
   	3 - 1

---

444. A vertical pole and a vertical tower are standing on the same level ground. Height of the pole is 10 metres. From the top of the pole the angle of elevation of the top of the tower and angle of depression of the foot of the tower are 60° and 30° respectively. The height of the tower is

1. 1. 20 m

   
   
   

   2. 30 m

   
   
   

   3. 40 m

   
   
   

   4. 50 m

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   AB = Pole = 10 metre
   CD = Tower = h metre (let)
   ∠ DAE = 60°
   ∠ EAC = ∠ ACB = 30°
   From ∆ ABC,
   

   tan 30° =	AB
   	BC

   
   

   ⇒	1	=	10
   	√3		BC

   
   ⇒ BC = 10 √3 metre
   ∴ AE = 10 √3 metre
   From ∆ ADE
   

   tan 60° =	DE
   	AE

   
   

   ⇒ √3 =	DE
   	10√3

   
   ⇒ DE = 10 √3 × √3
   = 30 metre
   ∴ CD = Heigth of tower
   = CE + ED = 10 + 30
   = 40 metre

   Correct Option: C

   
   AB = Pole = 10 metre
   CD = Tower = h metre (let)
   ∠ DAE = 60°
   ∠ EAC = ∠ ACB = 30°
   From ∆ ABC,
   

   tan 30° =	AB
   	BC

   
   

   ⇒	1	=	10
   	√3		BC

   
   ⇒ BC = 10 √3 metre
   ∴ AE = 10 √3 metre
   From ∆ ADE
   

   tan 60° =	DE
   	AE

   
   

   ⇒ √3 =	DE
   	10√3

   
   ⇒ DE = 10 √3 × √3
   = 30 metre
   ∴ CD = Heigth of tower
   = CE + ED = 10 + 30
   = 40 metre

---

---

445. The angle of elevation of sun changes from 30° to 45°, the length of the shadow of a pole decreases by 4 metres, the height of the pole is
     ( Assume √3 = 1.732)

1. 1. 1.464 m

   
   
   

   2. 9.464 m

   
   
   

   3. 3.648 cm

   
   
   

   4. 5.464 m

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
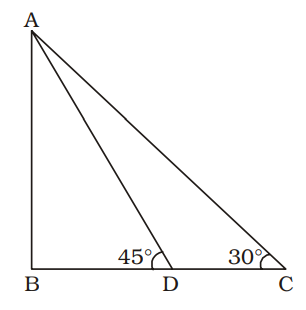
   ∠ACB = 30°
   ∠ADB = 45°
   CD = 4 metre
   AB = pole = h metre
   BD = x metre
   From ∆ABD
   

   tan 45° =	AB
   	BD

   
   

   ⇒ 1 =	h	⇒ h = x ......(i)
   	x

   
   From ∆ABC,
   

   tan 30° =	AB
   	BC

   
   

   ⇒	1	=	h
   	√3		x + 4

   
   

   ⇒	1	=	h	⇒ h + 4
   	√3		h + 4

   
   = √3h
   ⇒ √3h - h = 4
   ⇒ h( √3 - 1) = 4
   

   ⇒ h =	4	=	4(√3 + 1)
   	√3 - 1		(√3 - 1)(√3 + 1)

   
   = 2 (1.732 + 1)
   = 2 × 2.732
   = 5.464 metre

   Correct Option: D

   
   ∠ACB = 30°
   ∠ADB = 45°
   CD = 4 metre
   AB = pole = h metre
   BD = x metre
   From ∆ABD
   

   tan 45° =	AB
   	BD

   
   

   ⇒ 1 =	h	⇒ h = x ......(i)
   	x

   
   From ∆ABC,
   

   tan 30° =	AB
   	BC

   
   

   ⇒	1	=	h
   	√3		x + 4

   
   

   ⇒	1	=	h	⇒ h + 4
   	√3		h + 4

   
   = √3h
   ⇒ √3h - h = 4
   ⇒ h( √3 - 1) = 4
   

   ⇒ h =	4	=	4(√3 + 1)
   	√3 - 1		(√3 - 1)(√3 + 1)

   
   = 2 (1.732 + 1)
   = 2 × 2.732
   = 5.464 metre

---