Trigonometry
- If x = a sec θ and y = b tan θ then
a² - b² = ? x² y²
-
View Hint View Answer Discuss in Forum
x = a sec θ
⇒ x = sec θ a
Again, y = b tan θ⇒ y = tan θ b ∴ x² - y² a² b²
= sec² θ – tan² θ = 1Correct Option: A
x = a sec θ
⇒ x = sec θ a
Again, y = b tan θ⇒ y = tan θ b ∴ x² - y² a² b²
= sec² θ – tan² θ = 1
- The value of sin²1° + sin²2° + sin²3° + .....+ sin²89° is
-
View Hint View Answer Discuss in Forum
sin² 1° + sin² 2° + sin² 3° + ..... + sin² 89°
= (sin² 1° + sin² 89°) + (sin² 2° + sin² 88°) + .... to 44 terms + sin² 45°
= (sin² 1° + sin² (90° – 1°) + (sin² 2° + sin² (90° – 2°) +....to 44terms + 
1 
² √2 = (sin² 1° + cos² 1°) + (sin² 2° + cos² 2°) + ....to 44 terms + 1 [sin²θ + cos²θ = 1] 2 = 44 + 1 = 44 1 2 2
Correct Option: D
sin² 1° + sin² 2° + sin² 3° + ..... + sin² 89°
= (sin² 1° + sin² 89°) + (sin² 2° + sin² 88°) + .... to 44 terms + sin² 45°
= (sin² 1° + sin² (90° – 1°) + (sin² 2° + sin² (90° – 2°) +....to 44terms + 
1 
² √2 = (sin² 1° + cos² 1°) + (sin² 2° + cos² 2°) + ....to 44 terms + 1 [sin²θ + cos²θ = 1] 2 = 44 + 1 = 44 1 2 2
-
The value of cos3θ + sin3θ - cos3θ - sin3θ is equal to cosθ + sinθ cosθ - sinθ
-
View Hint View Answer Discuss in Forum
cos3θ + sin3θ + cos3θ - sin3θ cos θ + sinθ cos θ - sinθ = (cos θ + sin θ)(cos²θ + sin²θ - cos θ . sin θ) cos θ + sin θ = (cos θ - sin θ)(cos²θ + sin²θ + cos θ . sin θ) cos θ - sin θ
= cos²θ + sin²θ – cosθ . sinθ + cos²θ + sin²θ + cosθ . sinθ
= 1 + 1 = 2Correct Option: C
cos3θ + sin3θ + cos3θ - sin3θ cos θ + sinθ cos θ - sinθ = (cos θ + sin θ)(cos²θ + sin²θ - cos θ . sin θ) cos θ + sin θ = (cos θ - sin θ)(cos²θ + sin²θ + cos θ . sin θ) cos θ - sin θ
= cos²θ + sin²θ – cosθ . sinθ + cos²θ + sin²θ + cosθ . sinθ
= 1 + 1 = 2
- If sin 17° = (x / y) , then sec 17° – sin 73° is equal to
-
View Hint View Answer Discuss in Forum
sin 17° = x y
sin 73° = sin (90° – 17°)
= cos 17°
∴ cos 17° = √1 - sin² 17°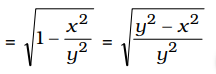
= √y² - x² y ∴ sec 17° = y √y² - x²
∴ sec 17° – sin 73°
= sec 17° – cos 17°y - √y² - x² √y² - x² y = y² - (y² - x²) y√y² - x² = y² - y² + x² y√y² - x² = y y√y² - x²
Correct Option: D
sin 17° = x y
sin 73° = sin (90° – 17°)
= cos 17°
∴ cos 17° = √1 - sin² 17°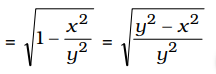
= √y² - x² y ∴ sec 17° = y √y² - x²
∴ sec 17° – sin 73°
= sec 17° – cos 17°y - √y² - x² √y² - x² y = y² - (y² - x²) y√y² - x² = y² - y² + x² y√y² - x² = y y√y² - x²
- If θ is a positive acute angle and cosec θ + cot θ = √3 , then the value of cosec θ is
-
View Hint View Answer Discuss in Forum
cosecθ + cotθ = 3 ...(i)
cosec²θ – cot²θ = 1
⇒ (cosecθ + cotθ) (cosecθ – cotθ) = 1⇒ cosecθ - cotθ = 1 ....(ii) √3 ∴ cosecθ + cotθ + cosecθ – cotθ = √3 + 1 √3 ⇒ 2 cosecθ = 3 + 1 √3 ⇒ cosecθ = 4 = 2 2√3 √3
Correct Option: C
cosecθ + cotθ = 3 ...(i)
cosec²θ – cot²θ = 1
⇒ (cosecθ + cotθ) (cosecθ – cotθ) = 1⇒ cosecθ - cotθ = 1 ....(ii) √3 ∴ cosecθ + cotθ + cosecθ – cotθ = √3 + 1 √3 ⇒ 2 cosecθ = 3 + 1 √3 ⇒ cosecθ = 4 = 2 2√3 √3

