Trigonometry
- The angle of elevation of the top of a building from the top and bottom of a tree are x and y respectively. If the height of the tree is h metre, then (in metre) the height of the building is
-
View Hint View Answer Discuss in Forum
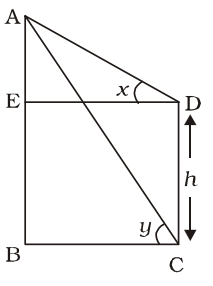
CD = tree = h metre
Let AB = building = a metre
& BC = ED = b metre
∴ From ∆ AED,tanx = AE ED ⇒ tan x = a - h b
⇒ b = (a – h) cot x ..........(i)
From ∆ ABC,tany = AB BC ⇒ tan y = a b
⇒ b = a cot y ...........(ii)
From equations (i) and (ii),
(a – h) cot x = a cot y
⇒ a cot x – h cot x = a cot y
⇒ h cot x = a (cot x – cot y)⇒ a = h cot x cot x - cot y Correct Option: C

CD = tree = h metre
Let AB = building = a metre
& BC = ED = b metre
∴ From ∆ AED,tanx = AE ED ⇒ tan x = a - h b
⇒ b = (a – h) cot x ..........(i)
From ∆ ABC,tany = AB BC ⇒ tan y = a b
⇒ b = a cot y ...........(ii)
From equations (i) and (ii),
(a – h) cot x = a cot y
⇒ a cot x – h cot x = a cot y
⇒ h cot x = a (cot x – cot y)⇒ a = h cot x cot x - cot y
- The distance between two pillars of length 16 metres and 9 metres is x metres. If two angles of elevation of their respective top from the bottom of the other are complementary to each other, then the value of x (in metres) is
-
View Hint View Answer Discuss in Forum
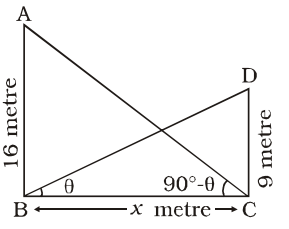
From ∆ABC,tan (90° – θ) = 16 x ⇒ cotθ = 16 ........(i) x
From ∆BCD,tanθ = 9 ........(ii) x ∴ tanθ . cotθ = 9 × 16 x x
⇒ x2 = 16 × 9 [∵ tanθ cotθ =1]
⇒ x = 4 × 3 = 12 metreCorrect Option: C

From ∆ABC,tan (90° – θ) = 16 x ⇒ cotθ = 16 ........(i) x
From ∆BCD,tanθ = 9 ........(ii) x ∴ tanθ . cotθ = 9 × 16 x x
⇒ x2 = 16 × 9 [∵ tanθ cotθ =1]
⇒ x = 4 × 3 = 12 metre
- At a point on a horizontal line through the base of a monument, the angle of elevation of the top of the monument is found to be such that its tangent is 1/5. On walking 138 metres towards the monument the secant of the angle of elevation is found to be
The height of the monument (in metre) is√193 . 12
-
View Hint View Answer Discuss in Forum
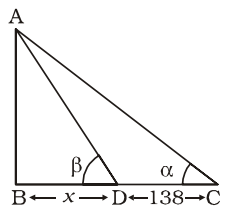
AB = monument = h metre
DC = 138 metre
BD = x metretan α = 1 5 sec β = √193 12
∴ tan β = √sec2 β - 1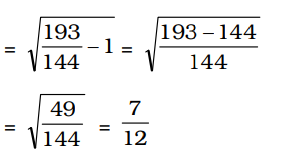
∴ From ∆ABC,tan α = AB BC ⇒ 1 = h 5 x + 138 ⇒ h = x + 138 5
⇒ 5h = x + 138 .............. (i)
From ∆ ABD,tan β = h ⇒ 7 = h x 12 x ⇒ x = 12h .........(ii) 7 ∴ 5h = 12h + 138 (By (i) & (ii) 7
⇒ 35h – 12h = 138 × 7
⇒ 23 h = 138 × 7⇒ h = 138 × 7 = 42 metre 23 Correct Option: C

AB = monument = h metre
DC = 138 metre
BD = x metretan α = 1 5 sec β = √193 12
∴ tan β = √sec2 β - 1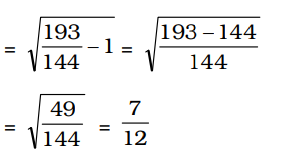
∴ From ∆ABC,tan α = AB BC ⇒ 1 = h 5 x + 138 ⇒ h = x + 138 5
⇒ 5h = x + 138 .............. (i)
From ∆ ABD,tan β = h ⇒ 7 = h x 12 x ⇒ x = 12h .........(ii) 7 ∴ 5h = 12h + 138 (By (i) & (ii) 7
⇒ 35h – 12h = 138 × 7
⇒ 23 h = 138 × 7⇒ h = 138 × 7 = 42 metre 23
- The angle of elevation of the top of a tower from two points A and B lying on the horizontal through the foot of the tower are respectively 15° and 30°. If A and B are on the same side of the tower and AB = 48 metre, then the height of the tower is :
-
View Hint View Answer Discuss in Forum
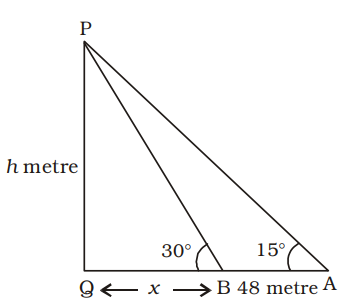
Tower = PQ = h metre
QB = x metre
From ∆ APQ,tan15° = h x + 48 2 – √3 = h ....(i) x + 48
[∵ tan 15° = tan (45° – 30°)= = 1 - 1 tan 45° - tan 30° √3 1 + tan 45°tan 30° 1 + 1 √3 or √3 - 1 × √3 - 1 √3 + 1 √3 - 1 = 4 - 2√3 = 2 - √3 ] 2
From ∆PQB,tan30° = h x ⇒ 1 = h √3 x
⇒ √3h = x .............(ii)⇒ 2 - √3 = h √3h + 48
⇒ 2√3h - 3h + (2 - √3) 48 = h
⇒ h + 3h - 2√3h
=(2 - √3) × 48
⇒ 2h(2 - √3) = 48 × ( 2 - √3)⇒ h = 48 = 24 metre 2 Correct Option: B

Tower = PQ = h metre
QB = x metre
From ∆ APQ,tan15° = h x + 48 2 – √3 = h ....(i) x + 48
[∵ tan 15° = tan (45° – 30°)= = 1 - 1 tan 45° - tan 30° √3 1 + tan 45°tan 30° 1 + 1 √3 or √3 - 1 × √3 - 1 √3 + 1 √3 - 1 = 4 - 2√3 = 2 - √3 ] 2
From ∆PQB,tan30° = h x ⇒ 1 = h √3 x
⇒ √3h = x .............(ii)⇒ 2 - √3 = h √3h + 48
⇒ 2√3h - 3h + (2 - √3) 48 = h
⇒ h + 3h - 2√3h
=(2 - √3) × 48
⇒ 2h(2 - √3) = 48 × ( 2 - √3)⇒ h = 48 = 24 metre 2
- One flies a kite with a thread 150 metre long. If the thread of the kite makes an angle of 60° with the horizontal line, then the height of the kite from the ground (assuming the thread to be in a straight line) is
-
View Hint View Answer Discuss in Forum
AB = Length of the thread = 150 metre
∆ BAC = 60°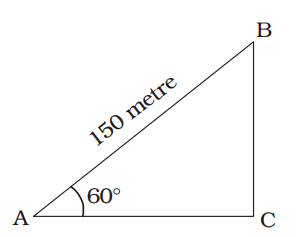
In ∆ ABC,sin 60° = BC ⇒ √3 = BC AB 2 150 ⇒ BC = 150 × √3 = 75√3 metre 2 Correct Option: B
AB = Length of the thread = 150 metre
∆ BAC = 60°
In ∆ ABC,sin 60° = BC ⇒ √3 = BC AB 2 150 ⇒ BC = 150 × √3 = 75√3 metre 2

