Materials Science and Manufacturing Engineering Miscellaneous
- For tool A, Taylor's tool life exponent (n) is 0.45 and constant (K) is 90. Similarly for tool B, n = 0.3 and K = 60. The cutting speed (in 'm/ min) above which tool A will have a higher tool life than tool B is
-
View Hint View Answer Discuss in Forum
Taylor’s tool life equation is
VTn = Constant
∴ k1 = v1T1n1 and k2 = v2T2n2
Given conditions for both tools:
Tool A : constant, k1 = 90 ;
exponential constant, n1 = 0.45
Tool B: Constant, k2 = 60 ;
exponential constant, x2 = 0.3∴ 
k1 
= 
v1 
T10.45 k2 v2 T20.3
At point of intersection
v1 = v2 and T1 = T2 = T∴ 3 = T0.45 = T0.15 2 T0.3
⇒ T = (3/2)1/0.15 = 14.92 min
∴ 90= v1(14.92)0.45
⇒ v1 = 26.7 m/min
Above v1 = 26.7 m/min, tool A will have a higher tool life them too B.Correct Option: A
Taylor’s tool life equation is
VTn = Constant
∴ k1 = v1T1n1 and k2 = v2T2n2
Given conditions for both tools:
Tool A : constant, k1 = 90 ;
exponential constant, n1 = 0.45
Tool B: Constant, k2 = 60 ;
exponential constant, x2 = 0.3∴ 
k1 
= 
v1 
T10.45 k2 v2 T20.3
At point of intersection
v1 = v2 and T1 = T2 = T∴ 3 = T0.45 = T0.15 2 T0.3
⇒ T = (3/2)1/0.15 = 14.92 min
∴ 90= v1(14.92)0.45
⇒ v1 = 26.7 m/min
Above v1 = 26.7 m/min, tool A will have a higher tool life them too B.
Direction: In a machining experiment, tool life was found to vary with the cutting speed in the following manner:
| Cutting speed (m/min) | Tool life (minutes) |
| 60 | 81 |
| 90 | 36 |
- What is the percentage increase in tool life when the cutting speed is halved?
-
View Hint View Answer Discuss in Forum
VTn = C
∴ Tn = C V or T = 
C 
1/n = 
C 
2 V V or T ∝ 1 V2 ∴ T0 = V2 T V02 ∴ T0 = (V0/2)2 T V02 or T0 – 1 = 4 – 1 T
Hence percent increase = 300%
Alternately:
When cutting speed is halved60 × (8.1)0.5 = 60 = (T2)0.5 2 or T2 = (2)2 81
or T2 =4 × 81% change in tool life = T2 − T1 T1 = (4 × 81) − 81 × 100 81 = 3 × 81 × 100 = 300% 81 Correct Option: C
VTn = C
∴ Tn = C V or T = 
C 
1/n = 
C 
2 V V or T ∝ 1 V2 ∴ T0 = V2 T V02 ∴ T0 = (V0/2)2 T V02 or T0 – 1 = 4 – 1 T
Hence percent increase = 300%
Alternately:
When cutting speed is halved60 × (8.1)0.5 = 60 = (T2)0.5 2 or T2 = (2)2 81
or T2 =4 × 81% change in tool life = T2 − T1 T1 = (4 × 81) − 81 × 100 81 = 3 × 81 × 100 = 300% 81
- The exponent (n) and constant (k) of the Taylor's tool life equation are
-
View Hint View Answer Discuss in Forum
According to Taylor’s equation
VTn = C
where, V = cutting speed in m/s
T = tool life (min)
C = constant (Taylors constant)
∴ V1T1n = V2T2n
or 60 × (81)n = 90 × (36)nor 60 = 
36 
n 90 81 or 2 = 
4 
n 3 9
Taking log of both sideslog 2 = n log 4 3 9 ∴ n = log 2 = 0.5 3 log 4 9
∴ Taylor’s constant C = V1T1n
= 60 × (81)0.5
= 60√81= 60 × 9 = 540Correct Option: A
According to Taylor’s equation
VTn = C
where, V = cutting speed in m/s
T = tool life (min)
C = constant (Taylors constant)
∴ V1T1n = V2T2n
or 60 × (81)n = 90 × (36)nor 60 = 
36 
n 90 81 or 2 = 
4 
n 3 9
Taking log of both sideslog 2 = n log 4 3 9 ∴ n = log 2 = 0.5 3 log 4 9
∴ Taylor’s constant C = V1T1n
= 60 × (81)0.5
= 60√81= 60 × 9 = 540
- Friction at the tool-chip interface can be reduced by
-
View Hint View Answer Discuss in Forum
By increasing the cutting speed. Heat dissipation is increased hence there is lower temperature & lower friction coefficient.
Correct Option: D
By increasing the cutting speed. Heat dissipation is increased hence there is lower temperature & lower friction coefficient.
Direction: Orthogonal turning is performed on a cylindrical workpiece with shear strength of 250 MPa. The following conditions are used: cutting velocity is 180 m/min, feed is 0.20 mm/rev, depth of cut is 3 mm, chip thickness ratio = 0.5. The orthogonal rake angle is 7°. Apply Merchants theory for analysis.
- The cutting and thrust forces, respectively, are
-
View Hint View Answer Discuss in Forum
FH = FS 
cos(β − α) 
cos(φ β α)
where β is friction L.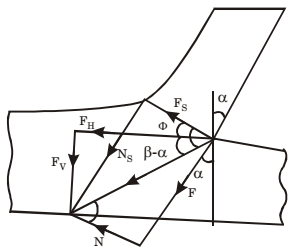
Now by Merchant’s theoryφ = π − 1 = (β − α) 4 2 ∴ 28 = 45° – β + 3.5° 2
∴ β = 2(20.5) = 41°∴ FH = FC 
cos(34) 
= 320 × 1.77 = 565 N cos(62) Now, FV = tan(β − α) FH
∴ FV = 565 × tan 34 = 381 N
Frictional force F from the figure can be written as,
F = FH sin + FV cos α
= 68 + 381 = 447N Hence none of the options seems to be correct.Correct Option: B
FH = FS 
cos(β − α) 
cos(φ β α)
where β is friction L.
Now by Merchant’s theoryφ = π − 1 = (β − α) 4 2 ∴ 28 = 45° – β + 3.5° 2
∴ β = 2(20.5) = 41°∴ FH = FC 
cos(34) 
= 320 × 1.77 = 565 N cos(62) Now, FV = tan(β − α) FH
∴ FV = 565 × tan 34 = 381 N
Frictional force F from the figure can be written as,
F = FH sin + FV cos α
= 68 + 381 = 447N Hence none of the options seems to be correct.

