Materials Science and Manufacturing Engineering Miscellaneous
- The transformation matrix for mirroring a point in x-y plane about the line y = x is given by
-
View Hint View Answer Discuss in Forum
For a reflection in the line y = x

0 1 
1 0
Correct Option: D
For a reflection in the line y = x

0 1 
1 0
- A point P(1, 3, -5) is translated by 2î + 3ˆk + 4ĵ and then rotated counter clockwise by 90° about the z-axis. The new position of the point is:
-
View Hint View Answer Discuss in Forum
P = (1, 3, – 5)
First translated by 2î + 3ĵ - 4ˆk and them rotate about z – axis by 90°
Homogeneous Translation Matrix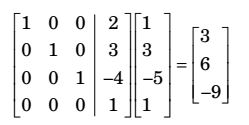
Then rotated about Z – axis.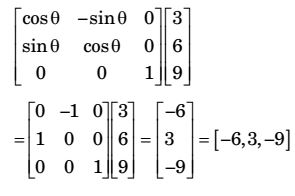
Correct Option: A
P = (1, 3, – 5)
First translated by 2î + 3ĵ - 4ˆk and them rotate about z – axis by 90°
Homogeneous Translation Matrix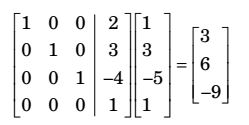
Then rotated about Z – axis.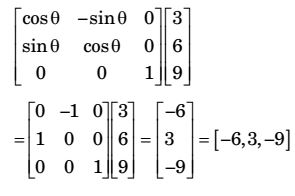
- For the situation shown in the figure below the expression for H in terms of r, R and D is

-
View Hint View Answer Discuss in Forum
AB = √(R + r)² - (D - R - r)²
H = R + AB + r
H = R + r + √(R + r + D - R - r) - (R + r - D + R + r)
H = R + r + √D[2(R + r) - D]
H = R + r + √[2D(R + r) - D²]Correct Option: D
AB = √(R + r)² - (D - R - r)²
H = R + AB + r
H = R + r + √(R + r + D - R - r) - (R + r - D + R + r)
H = R + r + √D[2(R + r) - D]
H = R + r + √[2D(R + r) - D²]
- The figure below represents a triangle PQR with initial coordinates of the vertices as P(1, 3), Q(4, 5) and ft(5.3.5). The triangle is rotated in X-Y plane about the vertex P by angle θ in clockwise direction. If sinθ = 0.6 and cosθ = 0.8, the new coordinates of the vertex Q are

-
View Hint View Answer Discuss in Forum
If the ∆PQR rotator by θ Clockwise then abscissa value of Q must increase whereas ordinate value of Q must decreases and only satisfying option is (4.6, 2.8) i.e. A.

Correct Option: A
If the ∆PQR rotator by θ Clockwise then abscissa value of Q must increase whereas ordinate value of Q must decreases and only satisfying option is (4.6, 2.8) i.e. A.

- A triangular face in a CAD model has vertices: P1(0, 0, 0); P2(1, 1, 0) and P3(1,1, 1).The area of the facet is
-
View Hint View Answer Discuss in Forum

Area = 1 × √2 × 1 = √2 = 0.707 2 2 Correct Option: B

Area = 1 × √2 × 1 = √2 = 0.707 2 2

