-
The angle of elevation of the top of a tower from a point on the ground is 30° and moving 70 metres towards the tower it becomes 60°. The height of the tower is
-
- 10 metre
-
10 metre √3 - 10 √3 metre
- 35 √3 metre
Correct Option: D
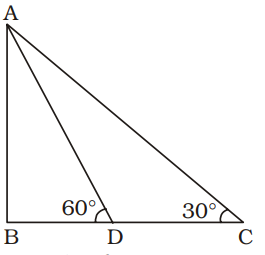
AB = Height of tower = h metre (let)
CD = 70 metre
BD = x metre (let)
In ∆ABC,
| tan30° = | BC |
| = | = | |||
| √3 | x + 70 |
⇒ √3h = x + 70
⇒ x = √3h – 70 ............(i)
In ∆ABD,
| tan60° = | x |
| ⇒ √3 = | x |
| ⇒ x = | .........(ii) | √3 |
From equations (i) and (ii),
| ⇒ √3 - 70 = | √3 |
| ⇒ √3h - | = 70 | √3 |
| = | = 70 | √3 |
⇒ 2h = 70 √3
| ⇒ h = | = 35 √3 metre | 2 |

