-
The angle of elevation of the top of a building from the top and bottom of a tree are x and y respectively. If the height of the tree is h metre, then (in metre) the height of the building is
-
-
h cot x cot x + cot y -
h cot y cot x + cot y -
h cot x cot x - cot y -
h cot y cot x - cot y
-
Correct Option: C
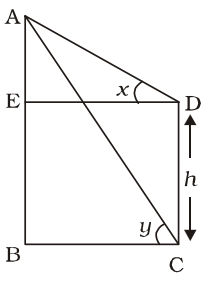
CD = tree = h metre
Let AB = building = a metre
& BC = ED = b metre
∴ From ∆ AED,
| tanx = | ED |
| ⇒ tan x = | b |
⇒ b = (a – h) cot x ..........(i)
From ∆ ABC,
| tany = | BC |
| ⇒ tan y = | b |
⇒ b = a cot y ...........(ii)
From equations (i) and (ii),
(a – h) cot x = a cot y
⇒ a cot x – h cot x = a cot y
⇒ h cot x = a (cot x – cot y)
| ⇒ a = | cot x - cot y |

