-
The angle of elevation of the top of a tower from two points A and B lying on the horizontal through the foot of the tower are respectively 15° and 30°. If A and B are on the same side of the tower and AB = 48 metre, then the height of the tower is :
-
- 24 √3 metre
- 24 metre
- 24 √3 metre
- 96 metre
Correct Option: B
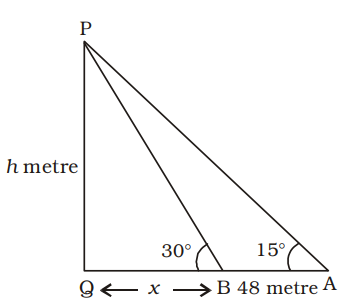
Tower = PQ = h metre
QB = x metre
From ∆ APQ,
| tan15° = | x + 48 |
| 2 – √3 = | ....(i) | x + 48 |
[∵ tan 15° = tan (45° – 30°)
| = | = | 1 - | |||||
| tan 45° - tan 30° | √3 | ||||||
| 1 + tan 45°tan 30° | 1 + | ||||||
| √3 | |||||||
| or | × | |||
| √3 + 1 | √3 - 1 |
| = | = 2 - √3 ] | 2 |
From ∆PQB,
| tan30° = | x |
| ⇒ | = | |||
| √3 | x |
⇒ √3h = x .............(ii)
| ⇒ 2 - √3 = | √3h + 48 |
⇒ 2√3h - 3h + (2 - √3) 48 = h
⇒ h + 3h - 2√3h
=(2 - √3) × 48
⇒ 2h(2 - √3) = 48 × ( 2 - √3)
| ⇒ h = | = 24 metre | 2 |

