Strength Of Materials Miscellaneous
- A thin walled spherical shell is subjected to an internal pressure. If the radius of the shell is increased by 1% and the thickness is reduced by 1%, with the internal pressure remaining the same, the percentage change in the circumferential (hoop) stress is
-
View Hint View Answer Discuss in Forum
Hoop stress for a thin spherical shell
σh = Pr 2t
Applying logarithm on both sides, we getlog(σh) = log 
P 
+ log(r) - log(t) 2
Differentiating above equation,dσh = 0 + dr - dt σh r t Given : dr = 0.01 and dt = -0.01 r t
Substituting, we getdσh = 0.02 σh
Hence percentage increase will be 2%.Correct Option: D
Hoop stress for a thin spherical shell
σh = Pr 2t
Applying logarithm on both sides, we getlog(σh) = log 
P 
+ log(r) - log(t) 2
Differentiating above equation,dσh = 0 + dr - dt σh r t Given : dr = 0.01 and dt = -0.01 r t
Substituting, we getdσh = 0.02 σh
Hence percentage increase will be 2%.
- A 6 meter long supported wooden beam of rectangular section 10 cm × 20 cm deep is strengthened by mild steel plates 0.5 cm x 10 cm wide at the top and bottom fibre over the entire length. Find the minimum supportable uniformly distributed load considering failures in steel and wood due to flexure. Weakening of wood due to screws and weakening of the steel plates due to drilled holes may be ignored
Permissible tensile stress for steel = 156.8 N/mm2
Permissible tensile stress for wood = 14.89 N/mm2
Young's modulus of mild steel = 1.96 × 105 N/mm2
Young's modulus of wood = 0.117 × 105 N/mm2
-
View Hint View Answer Discuss in Forum
Modular ratio , M = Es = 1.96 × 105 = 16.75 Et 0.117 × 105
Equivalent Steel area & width of timber= 200 × 100 = 5.97 mm 16.75 × 200 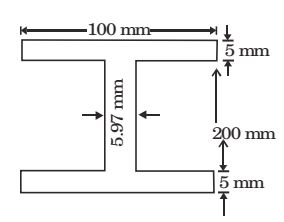
I = 100 × 2103 = 14.5 × 106 mm4 12 Stress in timber = 156.8 × 100 × 1 = 8.915 N/mm2 105 16.75
(If permissible stress in steal = 156.8 MPa)Stress in steel = 14.89 × 105 × 16.75 = 261.88 N / mm2 100
(If permissible stress in wood = 14.8 MPa) Imax = 156.8 MPaM = σ I y M = 156.8 × 14.5 × 106 = 21.65 Nm 105 wl2 = M = 2165 × 106 8
⇒ w = 4.81 kN/m.Correct Option: B
Modular ratio , M = Es = 1.96 × 105 = 16.75 Et 0.117 × 105
Equivalent Steel area & width of timber= 200 × 100 = 5.97 mm 16.75 × 200 
I = 100 × 2103 = 14.5 × 106 mm4 12 Stress in timber = 156.8 × 100 × 1 = 8.915 N/mm2 105 16.75
(If permissible stress in steal = 156.8 MPa)Stress in steel = 14.89 × 105 × 16.75 = 261.88 N / mm2 100
(If permissible stress in wood = 14.8 MPa) Imax = 156.8 MPaM = σ I y M = 156.8 × 14.5 × 106 = 21.65 Nm 105 wl2 = M = 2165 × 106 8
⇒ w = 4.81 kN/m.
- A tapered cantilever beam of constant thickness is loaded as shown in the sketch below. The bending stress will be
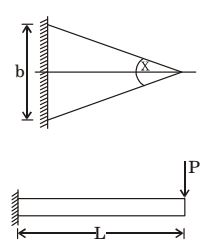
-
View Hint View Answer Discuss in Forum
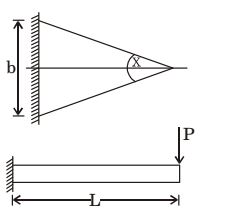
m = σ I y (PL / bd3) = (σ / d) 12 2 σ = 6PL bd2
Correct Option: D

m = σ I y (PL / bd3) = (σ / d) 12 2 σ = 6PL bd2
- Which one of the following diagrams shows correctly the distribution of transverse shear stress across the depth h of a rectangular beam subjected to varying bending moment along its length?
-
View Hint View Answer Discuss in Forum
Transverse shear stress distribution on a rectangular cross section due to varying bending moment is
q = F 
d2 - y2 
2l 4
Correct Option: B
Transverse shear stress distribution on a rectangular cross section due to varying bending moment is
q = F 
d2 - y2 
2l 4
- The second moment of a circular area about the diameter is given by (D is the diameter)
-
View Hint View Answer Discuss in Forum
Polar Moment of Inertia perpendicular to the plane of paper.
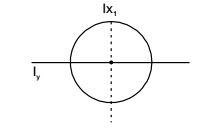
Ip = πD4 32
Now, applying “Perpendicular Axes” Theorem.
Ix + Iy = Ip
⇒ 2Ix = Ip⇒ Ix = Ip [ ∵ Ix = Iy ] 2 = πD4 64 Correct Option: D
Polar Moment of Inertia perpendicular to the plane of paper.

Ip = πD4 32
Now, applying “Perpendicular Axes” Theorem.
Ix + Iy = Ip
⇒ 2Ix = Ip⇒ Ix = Ip [ ∵ Ix = Iy ] 2 = πD4 64

