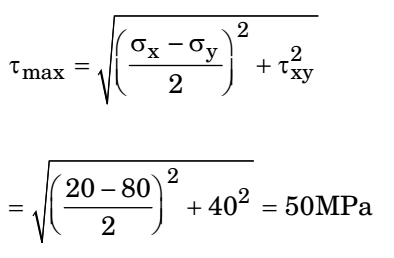31. For a simply supported beam on two end supports, the bending moment is maximum

1. 1. usually on the supports

   
   
   

   2. always at mid span

   
   
   

   3. where there is no shear force

   
   
   

   4. where the deflection is maximum

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Bending moment is maximum where shear force is zero.

   Correct Option: C

   Bending moment is maximum where shear force is zero.

---

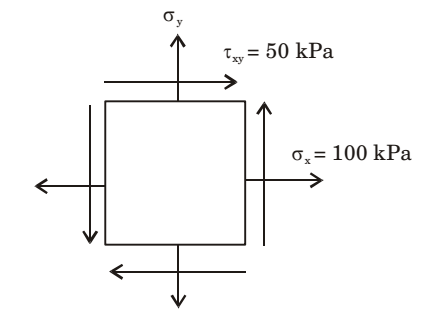
32. The State of stress at a point, for a body in place stress, is shown in the figure below. If the minimum principal stress is 10 kPa, then the normal stress σ_s (in kPa) is
    

1. 1. 9.45

   
   
   

   2. 18.88

   
   
   

   3. 37.78

   
   
   

   4. 75.50

   
   
   

---

1. View Hint View Answer Discuss in Forum

   σ_x = 100 kPa, τ_xy = 50 kPa
   Minimum principal stress
   
   By squaring
   

   2500 +	σy2	- 50σy + 2500 = 1600 +	σy2	+ 40σy
   	4		4

   
   ∴ 90 σ_y = 3400
   σ_y = 37.78 MPa

   Correct Option: C

   σ_x = 100 kPa, τ_xy = 50 kPa
   Minimum principal stress
   
   By squaring
   

   2500 +	σy2	- 50σy + 2500 = 1600 +	σy2	+ 40σy
   	4		4

   
   ∴ 90 σ_y = 3400
   σ_y = 37.78 MPa

---

---

33. The state of stress at a point is σ_x = σ_y = σ_z = τ_xz = τ_zx = τ_yx = τ_zy= 0 and τ_xy = τ_yx = 50 MPa. The maximum normal stress (in MPa) at that point is ______.

1. 1. 50

   
   
   

   2. 52

   
   
   

   3. 55

   
   
   

   4. 60

   
   
   

---

1. View Hint View Answer Discuss in Forum

   The state of stress is pure shear
   ∴ σ₁ = –σ₂ = τ = 50 MPa.
   σ_max = 50 MPa

   Correct Option: A

   The state of stress is pure shear
   ∴ σ₁ = –σ₂ = τ = 50 MPa.
   σ_max = 50 MPa

---

34. The state of stress at a point on an element is shown in figure (a). The same state of stress is shown in another coordinate system in figure (b).
    
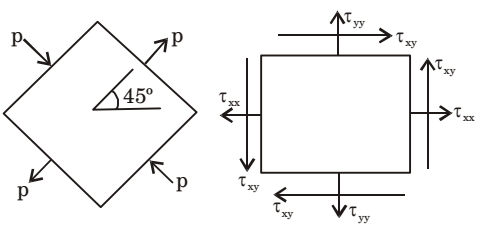
    The components (τ_xx, τ_yy, τ_xy,) are given by

1. 1. 		p	, -	p	, 0
      		√2		√2

   
   
   

   2. (0,0, p)

   
   
   

   3. 		p, - p,	p
      			√2

   
   
   

   4. 		0, 0,	p
      			√2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

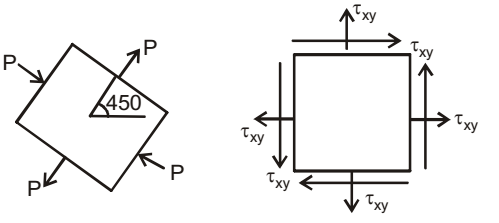
   σθ =		σx + σy		+		σx - σy		cos2θ + τxysine2θ
   		2				2

   
   Here θ = - 45
   σ_θ = T_xy
   σ_x = p
   σ_y = - p
   

   σθ =Txy =		P + P		+		P - P		cos90° = 0
   		2				2

   
   When θ = + 45
   

   σθ =		P - P		+		P + P		cos90°
   		2				2

   
   When θ = 45° T_θ = T_xy
   

   Tθ =		σx - σy		sin2θ - Txy cos2θ
   		2

   
   

   Tθ = Txy =		P + P		sin90° = P
   		2

   
   ∴ T_xx, T_yy, T_xy = 0, 0, p

   Correct Option: B

   
   

   σθ =		σx + σy		+		σx - σy		cos2θ + τxysine2θ
   		2				2

   
   Here θ = - 45
   σ_θ = T_xy
   σ_x = p
   σ_y = - p
   

   σθ =Txy =		P + P		+		P - P		cos90° = 0
   		2				2

   
   When θ = + 45
   

   σθ =		P - P		+		P + P		cos90°
   		2				2

   
   When θ = 45° T_θ = T_xy
   

   Tθ =		σx - σy		sin2θ - Txy cos2θ
   		2

   
   

   Tθ = Txy =		P + P		sin90° = P
   		2

   
   ∴ T_xx, T_yy, T_xy = 0, 0, p

---

---

35. In a plane stress condition, the components of stress at a point are σ_x = 20 MPa, σ_y = 80 MPa and σ_xy = 40 MPa. The maximum shear stress (in MPa) at the point is

1. 1. 20

   
   
   

   2. 25

   
   
   

   3. 50

   
   
   

   4. 100

   
   
   

---

1. View Hint View Answer Discuss in Forum

   

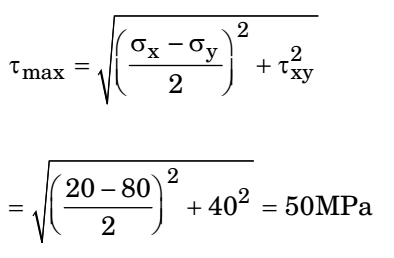
   Correct Option: C

   

---