81. Consider a cantilever beam, having negligible mass and uniform flexural rigidity, with length 0.01 m. The frequency of vibration of the beam, with a 0.5 kg mass attached at the free tip, is 100 Hz. The flexural rigidity (in Nm2) of the beam is ______.

1. 1. 0.065

   
   
   

   2. 0.650

   
   
   

   3. 0.66

   
   
   

   4. 0.066

   
   
   

---

1. View Hint View Answer Discuss in Forum

   S =	FL3
   	3EI

   
   

   k =	F		3EI
   	S		L3

   
   

   k =	3EI
   	(0.01)3

   
   k = 3, 000, 000 EI
   

   Correct Option: A

   S =	FL3
   	3EI

   
   

   k =	F		3EI
   	S		L3

   
   

   k =	3EI
   	(0.01)3

   
   k = 3, 000, 000 EI
   

---

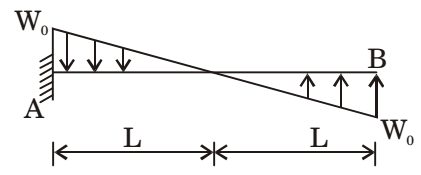
82. A cantilever beam carries the anti symmetric load shown, where W₀ is the peak intensity of the distributed load. Qualitatively, the correct bending moment diagram for this beam is
    

1. 1. 

   
   
   

   2. 

   
   
   

   3. 

   
   
   

   4. 

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   Here at both the ends, slope is zero and SF is zero. As moving form left to right, rate of shear force decreases due to varying uniform distributed load.

   Correct Option: C

   
   Here at both the ends, slope is zero and SF is zero. As moving form left to right, rate of shear force decreases due to varying uniform distributed load.

---

---

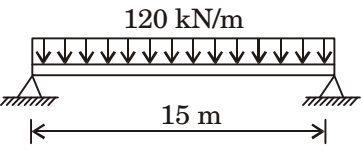
83. The value of maximum deflection of the beam is

1. 1. 93.75 mm

   
   
   

   2. 83.75 mm

   
   
   

   3. 73.75 mm

   
   
   

   4. 63.75 mm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Moment of inertia
   

   I =	bh3	=	120 × (750)3	= 42.1875 × 108 mm4
   	12		12

   
   Maximum deflection in the beam is given by
   

   δ =	5		wL4
   	384		EI

   
   

   =	5	×	120 × 103	×	(15 × 103)4
   	384		103		200 × 103 × 42.1875 × 108

   
   = 93.75 mm

   Correct Option: A

   Moment of inertia
   

   I =	bh3	=	120 × (750)3	= 42.1875 × 108 mm4
   	12		12

   
   Maximum deflection in the beam is given by
   

   δ =	5		wL4
   	384		EI

   
   

   =	5	×	120 × 103	×	(15 × 103)4
   	384		103		200 × 103 × 42.1875 × 108

   
   = 93.75 mm

---

84. The beam is subjected to a maximum bending moment of

1. 1. 3375 kNm

   
   
   

   2. 4750 kNm

   
   
   

   3. 6750 kNm

   
   
   

   4. 8750 kNm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Maximum bending moment occurs at the centre
   

   =	wL2	=	20 × (15)2	= 3375 kNm
   	8		8

   Correct Option: A

   Maximum bending moment occurs at the centre
   

   =	wL2	=	20 × (15)2	= 3375 kNm
   	8		8

---

---

85. A concentrated load P acts on a simply supported beam of span L at a distance L/3 from the left support. The bending moment at the point of application of the load is given by

1. 1. PL

      3

   
   
   

   2. 2PL

      3

   
   
   

   3. PL

      9

   
   
   

   4. 2PL

      9

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For horizontal equilibrium
   R₁ + R₂ = P
   Taking moment about R₁, we have
   R₂ × L = P × L/3
   

   R2 =	P
   	3

   
   

   ∴ R1 =	2P
   	3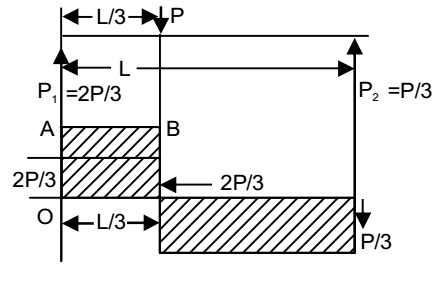

   
   
   The bending moment at the point of application of load = Area under OABC
   

   =	2P	×	L	=	2PL
   	3		3		9

   Correct Option: D

   For horizontal equilibrium
   R₁ + R₂ = P
   Taking moment about R₁, we have
   R₂ × L = P × L/3
   

   R2 =	P
   	3

   
   

   ∴ R1 =	2P
   	3

   
   
   The bending moment at the point of application of load = Area under OABC
   

   =	2P	×	L	=	2PL
   	3		3		9

---