Strength Of Materials Miscellaneous Easy Questions and Answers

Strength Of Materials Miscellaneous

Direction: A triangular-shaped cantilever beam of uniformthickness is shown in the figure. The Young's modulus of the material of the beam is E. A concentrated load P is applied at the free end of the beam.

The maximum deflection of the beam is

Maximum deflection of the beam

y_max =	Pl³	=	6Pl³
	3EI		Ebt³

where, I =	bt³
	18l

Correct Option: D

Maximum deflection of the beam

y_max =	Pl³	=	6Pl³
	3EI		Ebt³

where, I =	bt³
	18l

The area moment of inertia about the neutral axis of a cross-section at a distance x measured from the free end is

At a distance of x from the free end width

b' =	bx
	l

∴ Moment of Inertia I_x =	bxt³
	12l

Correct Option: B

At a distance of x from the free end width

b' =	bx
	l

∴ Moment of Inertia I_x =	bxt³
	12l

Direction: A massless beam has a loading pattern as shown in the figure. The beam is of rectangular crosssection with a width of 30 mm and height of 100 mm.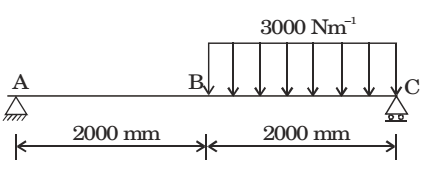

The maximum magnitude of bending stress (in MPa) is given by

M_{X = 2.5} = 1500(2.5) −	3000(2.5 − 2)²
	2

M = 3375 Nm.

M	=	σ
I	=	y

σ =	33752 ×	0.1	= 67.5MPa
		2

	0.03 × 0.13
	12

Correct Option: B

M_{X = 2.5} = 1500(2.5) −	3000(2.5 − 2)²
	2

M = 3375 Nm.

M	=	σ
I	=	y

σ =	33752 ×	0.1	= 67.5MPa
		2

	0.03 × 0.13
	12

The maximum bending moment occurs at

R_A = 1500 N
R_B = 4500 N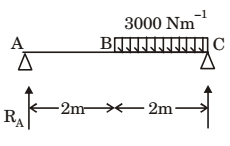

SF = R_A –3000 (x–2)
SF_x=2 = 1500 SF_x=4 = –4500
SF = 1500 – 3000 (x–2) = 0 [For max BM]
x = 2.5 m
x = 2500 mm from A.

Correct Option: C

R_A = 1500 N
R_B = 4500 N

SF = R_A –3000 (x–2)
SF_x=2 = 1500 SF_x=4 = –4500
SF = 1500 – 3000 (x–2) = 0 [For max BM]
x = 2.5 m
x = 2500 mm from A.

The maximum principal stress in MPa and the orientation of the corresponding principal plane in degrees are respectively

Maximum principal stress

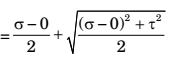
= 99.95 MPa.

Correct Option: B

Maximum principal stress

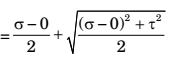
= 99.95 MPa.