116. For a loaded cantilever beam of uniform crosssection, the bending moment (in Nmm) along the length is M(x) = 5x² + 10x, where x is the distance (in mm) measured from the free end of the beam. The magnitude of shear force (in N) in the cross- section at x = 10 mm is _____.

1. 1. 110N

   
   
   

   2. 10N

   
   
   

   3. 120N

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   M(x) = 5x² + 10x
   

   Shear force(F) =	dM(x)
   	dx

   
   F_x = 10x + 10
   F_{(x = 10)} = 10(10) + 10 = 110N

   Correct Option: A

   M(x) = 5x² + 10x
   

   Shear force(F) =	dM(x)
   	dx

   
   F_x = 10x + 10
   F_{(x = 10)} = 10(10) + 10 = 110N

---

117. A simply supported beam of length L is subjected to a varying distributed load sin (3πx/L) Nm^-1, where the distance x is measured from the left support. The magnitude of the vertical reaction force in N at the left support is

1. 1. zero

   
   
   

   2. L/3π

   
   
   

   3. L/π

   
   
   

   4. 2 L/π

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
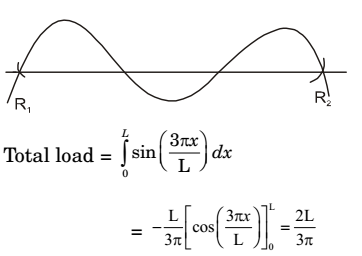
   By symmetry, R₁ = R₂ = P/2

   Correct Option: B

   
   By symmetry, R₁ = R₂ = P/2

---

---

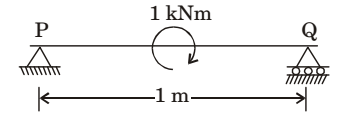
118. A simply supported beam PQ is loaded by a moment of 1 kNm at the mid-span of the beam as shown in the figure. The reaction forces R_p and R_Q at supports P and Q respectively are
     

1. 1. 1 kN downward, 1 kN upward

   
   
   

   2. 0.5 kN upward, 0.5 kN downward

   
   
   

   3. 0.5 kN downward, 0.5 kN upward

   
   
   

   4. 1 kN upward, 1 kN upward

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Take moments about ‘Q’
   R_Q × 1 – 1= 0
   ⇒  R_Q = 1kN ↑
   But   R_P + R_Q = 0
   ∴  R_P = – R_Q = – 1 kN
   ⇒  R_P = = 1kN ↓

   Correct Option: A

   Take moments about ‘Q’
   R_Q × 1 – 1= 0
   ⇒  R_Q = 1kN ↑
   But   R_P + R_Q = 0
   ∴  R_P = – R_Q = – 1 kN
   ⇒  R_P = = 1kN ↓

---

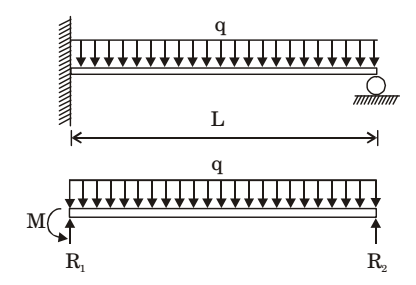
119. A uniformly loaded propped cantilever beam and its free body diagram are shown below. The reactions are
     

1. 1. R1 =	5qL	R2 =	3qL	,M =	qL²
      	8		8		8

   
   
   

   2. R1 =	3qL	,R2 =	5qL	,M =	qL²
      	8		8		8

   
   
   

   3. R1 =	5qL	,R2 =	3qL	,M = 0
      	8		8

   
   
   

   4. R1 =	3qL	,R2 =	5qL	,M = 0
      	8		8

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
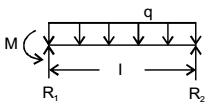
   R₁ + R₂ = ql     ...(i)
   Moment about (1),
   

   R2l +	ql²	− M      ...(ii)
   	6

   
   Moment about (2),
   

   R1l −	ql²	− M      ...(iii)
   	6

   
   From (i), (ii), (iii), we get
   

   R1 =	5ql	,R2 =	3ql	and M =	ql²
   	8		8		8

   Correct Option: A

   
   R₁ + R₂ = ql     ...(i)
   Moment about (1),
   

   R2l +	ql²	− M      ...(ii)
   	6

   
   Moment about (2),
   

   R1l −	ql²	− M      ...(iii)
   	6

   
   From (i), (ii), (iii), we get
   

   R1 =	5ql	,R2 =	3ql	and M =	ql²
   	8		8		8

---

---

120. A block of steel is loaded by a tangential force on its top surface while the bottom surface is held rigidly. The deformation of the block is due to
     

1. 1. shear only

   
   
   

   2. bending only

   
   
   

   3. shear and bending

   
   
   

   4. torsion

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: C

   NA

---