56. A circular metallic rod of length 250 mm is placed between two rigid immovable walls as shown in the figure. The rod is perfect contact with the wall on the left side and there is a gap of 0.2 mm between the rod and the wall on the right side. If the temperature of the rod is increased by 200°C, the axial stress developed in the rod is _______ MPa. Young's modulus of the material of the rod is 200 GPa and the coefficient of thermal expansion is10^-5per°C.
    

1. 1. 239.8 MPa

   
   
   

   2. 240.8 MPa

   
   
   

   3. 241.8 MPa

   
   
   

   4. 237.8 MPa

   
   
   

---

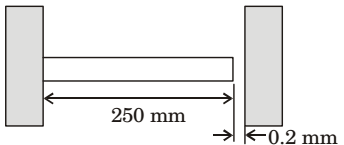
1. View Hint View Answer Discuss in Forum

   lαt = 250 × (10^–5)(200)
   

   =	1	= 0.5 mm > gap
   	2

   
   

   Deformation prevented = 0.5 – 0.2 = 0.3 =	Pl
   	AE

   
   

   ⇒ 0.3 =	σ(250 + 0.2)
   	200 × 103

   
   σ = 239.8 MPa

   Correct Option: A

   lαt = 250 × (10^–5)(200)
   

   =	1	= 0.5 mm > gap
   	2

   
   

   Deformation prevented = 0.5 – 0.2 = 0.3 =	Pl
   	AE

   
   

   ⇒ 0.3 =	σ(250 + 0.2)
   	200 × 103

   
   σ = 239.8 MPa

---

57. A 200 mm long, stress free rod at room temperature is held between two immovable rigid walls. The temperature of the rod is uniformly raised by 250°C. If the Young's modulus and coefficient of thermal expansion are 200 GPa and 1 × 10^-5/°C, respectively, the magnitude of the longitudinal stress (in MPa) developed in the rod is _______

1. 1. 500 MPa

   
   
   

   2. 4990 MPa

   
   
   

   3. 501 MPa

   
   
   

   4. 350 MPa

   
   
   

---

1. View Hint View Answer Discuss in Forum

   l = 200, ∆T = 250°C, α = 1 × 10^–5°c
   E = 200 GPa = 200 × 10³ MPa
   σ = α∆TE = 1 × 10^–5 × 250 × 200 × 103
   = 500 MPa.

   Correct Option: A

   l = 200, ∆T = 250°C, α = 1 × 10^–5°c
   E = 200 GPa = 200 × 10³ MPa
   σ = α∆TE = 1 × 10^–5 × 250 × 200 × 103
   = 500 MPa.

---

---

58. A steel cube, with all faces free to deform, has Young's modulus, E, Poisson's ratio, v, and coefficient of thermal expansion, a. The pressure (hydrostatic stress) developed within the cube, when it is subjected to a uniform increase in temperature, ∆T, is given by

1. 1. 0

   
   
   

   2. α(∆ T)E
      (1 - 2v)

   
   
   

   3. α(∆ T)E
      (1 - 2v)

   
   
   

   4. 	α(∆ T)E
      	3(1 - 2v)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Since all the faces are free to expand the stresses due to temperature rise is equal to 0.

   Correct Option: A

   Since all the faces are free to expand the stresses due to temperature rise is equal to 0.

---

59. A circular rod of length L and area of crosssection A has a modulus of elasticity E and coefficient of thermal expansion α. One end of the rod is fixed and other end is free. If the temperature of the rod is increased by ∆T, then

1. 1. stress developed in the rod is Eα∆T and strain developed in the rod is a ∆T

   
   
   

   2. both stress and strain developed in the rod are zero

   
   
   

   3. stress developed in the rod is zero and strain developed in the rod is α∆T

   
   
   

   4. stress developed in the rod is Eα∆T and strain developed in the rod is zero

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Since one end of the rod is fixed and other is free to expand. Hence the temperature stresses is zero
   

   ε	δL		α∆TL	= α∆T
   	L		L

   
   

   Correct Option: C

   Since one end of the rod is fixed and other is free to expand. Hence the temperature stresses is zero
   

   ε	δL		α∆TL	= α∆T
   	L		L

   
   

---

---

60. A solid steel cube constrained on all six faces is heated so that the temperature rises uniformly by ∆T. If the thermal coefficient of the material is α, Young's modulus is E and the Poisson's ratio is υ, the thermal stress developed in the cube due to heating is

1. 1. -	α(∆ T)E
      	(1 - 2v)

   
   
   

   2. -	2α(∆ T)E
      	(1 - 2v)

   
   
   

   3. -	3α(∆ T)E
      	(1 - 2v)

   
   
   

   4. -	α(∆ T)E
      	3(1 - 2v)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Volumetric strain
   

   ε V =	(1 - 2μ)	[σx + σy + σz]
   	E

   
   

   α ∆T =	(1 - 2μ)	(σ)
   	E

   
   

   σ =	α (∆T)E
   	(1 - 2μ)

   
   

   Correct Option: A

   Volumetric strain
   

   ε V =	(1 - 2μ)	[σx + σy + σz]
   	E

   
   

   α ∆T =	(1 - 2μ)	(σ)
   	E

   
   

   σ =	α (∆T)E
   	(1 - 2μ)

   
   

---