36. A horizontal bar, fixed at one end (x = 0), has a length of 1 m, and cross-sectional area of 100 mm². Its elastic modulus varies along its length as given by E(x) = 100e^–x GPa, where x is the length coordinate (in m) along the axis of the bar. An axial tensile load of 10 kN is applied at the free end (x = 1). The axial displacement of the free end is _____ mm.

1. 1. 1.788

   
   
   

   2. 0.718

   
   
   

   3. 1.718

   
   
   

   4. 2.718

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
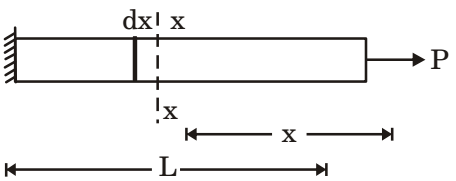
   Change in length of small strip
   

   δ =	Px - x(dx)
   	Ax - xEx - x

   
   Total change in length of bar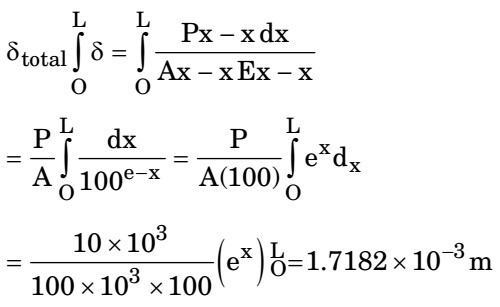
   
   δ = 1.718 mm

   Correct Option: C

   
   Change in length of small strip
   

   δ =	Px - x(dx)
   	Ax - xEx - x

   
   Total change in length of bar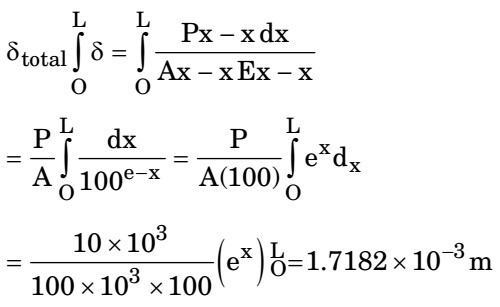
   
   δ = 1.718 mm

---

37. A rod is subjected to a uni-axial load within linear elastic limit. When the change in the stress is 200 MPa, the change in the strain is 0.001. If the Poisson's ratio of the rod is 0.3, the modulus of rigidity (in GPa) is

1. 1. 76.92

   
   
   

   2. 76.22

   
   
   

   3. 76.72

   
   
   

   4. 76

   
   
   

---

1. View Hint View Answer Discuss in Forum

   E	σ	+	200 × 106	= 200GPa
   	t		0.001

   
   

   G =	200	= 76.92GPa
   	2(1 + 0.3)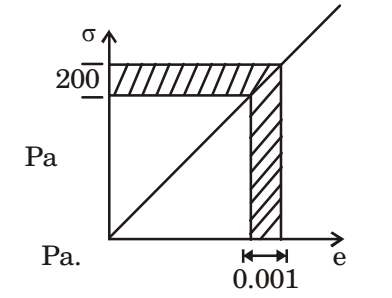

   
   

   Correct Option: A

   E	σ	+	200 × 106	= 200GPa
   	t		0.001

   
   

   G =	200	= 76.92GPa
   	2(1 + 0.3)

   
   

---

---

38. The number of independent elastic constants required to define the stress-strain relationship for an isotropic elastic solid is _____.

1. 1. G & μ are independent.

   
   
   

   2. E & μ are independent.

   
   
   

   3. G & E & μ are independent.

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Elastic constants are required to obtain relationship between stress & strain, There are 4 elastic constants.
   E, μ, G, & E
   But E & μ are independent.

   Correct Option: B

   Elastic constants are required to obtain relationship between stress & strain, There are 4 elastic constants.
   E, μ, G, & E
   But E & μ are independent.

---

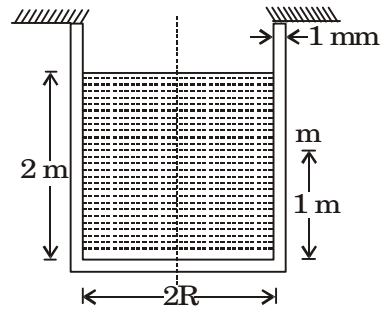
39. If the Young's modulus and Poisson's ratio of the container material' are 100 GPa and 0.3, respectively, the axial strain in the cylinder wall at mid-depth is

1. 1. 2 × 10^–5

   
   
   

   2. 6 × 10^–5

   
   
   

   3. 7 × 10^–5

   
   
   

   4. 1.2 × 10^–4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Axial strain in the cylinder would be produced due to the axial (longitudinal) stress and due to the lateral stress
   

   i.e.hoop stress, e =	1			σu -	σc
   	y				m

   
   

   =	1	(5 - 10 × 0.3)
   	100 × 103

   Correct Option: A

   Axial strain in the cylinder would be produced due to the axial (longitudinal) stress and due to the lateral stress
   

   i.e.hoop stress, e =	1			σu -	σc
   	y				m

   
   

   =	1	(5 - 10 × 0.3)
   	100 × 103

---

---

40. The axial and circumferential stress (σa, σc) experienced by the cylinder wall at mid-depth (m as shown) are

1. 1. (10,10) MPa

   
   
   

   2. (5,10) MPa

   
   
   

   3. (10,5)MPa

   
   
   

   4. (5, 5) MPa

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Pressure at mid – depth = ρgh = 10³ × 10 × 1 = 10⁴ N/m²
   

   ∴ σa =	pd	+	104 × 2
   	4t		4 × 10-3

   
   = 5 × 10⁶ N/mm² = 5 MPa
   

   σa =	pd	+	104 × 2	= 10MPa
   	2t		2 × 10-3

   Correct Option: B

   Pressure at mid – depth = ρgh = 10³ × 10 × 1 = 10⁴ N/m²
   

   ∴ σa =	pd	+	104 × 2
   	4t		4 × 10-3

   
   = 5 × 10⁶ N/mm² = 5 MPa
   

   σa =	pd	+	104 × 2	= 10MPa
   	2t		2 × 10-3

---