51. A machine element XY, fixed at end X, is subjected to an axial load P, transverse load F, and a twisting moment T at its free end Y. The most critical point from the strength point of view is
    

1. 1. a point on the circumference at location Y

   
   
   

   2. a point at the center at location Y

   
   
   

   3. a point on the circumference at location X

   
   
   

   4. a point at the center at location X

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   At centre σ_b = 0 and torsional shear stress are zero.

   Correct Option: C

   
   At centre σ_b = 0 and torsional shear stress are zero.

---

52. A shaft with a circular cross-section is subjected to pure twisting moment. The ratio of the maximum shear stress to the largest principal stress is

1. 1. 2.0

   
   
   

   2. 1.0

   
   
   

   3. 0.5

   
   
   

   4. 0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   τ_max = τ_xy
   σ₁ = τ_xy
   

   ∴	τmax	= 1
   	σ1

   Correct Option: B

   
   τ_max = τ_xy
   σ₁ = τ_xy
   

   ∴	τmax	= 1
   	σ1

---

---

53. A solid circular shaft of diameter d is subjected to a combined bending moment M and torque, T. The material property to be used for designing the shaft using the relation
    

    16	√M² + T² is
    πd³

1. 1. ultimate tensile strength (S_u)

   
   
   

   2. tensile yield strength (S_y)

   
   
   

   3. torsional yield strength (S_sy)

   
   
   

   4. endurance strength (S_e)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For a circular shaft of diameter d,
   

   T '	=	τ
   J		(d/2)

   
   where, T ' = net torsional moment
   τ = shear stress (torsional shear strength)
   J = polar moment of inertia
   

   ∴  t =	T '(d/2)
   	J

   
   But for a solid circular shaft
   

   J =	π	d4
   	32

   
   

   ∴  τ =	16T '
   	32

   
   But T ' = √M² + T²
   

   ∴  τ =	16T '	√M² + T²
   	πd3

   Correct Option: C

   For a circular shaft of diameter d,
   

   T '	=	τ
   J		(d/2)

   
   where, T ' = net torsional moment
   τ = shear stress (torsional shear strength)
   J = polar moment of inertia
   

   ∴  t =	T '(d/2)
   	J

   
   But for a solid circular shaft
   

   J =	π	d4
   	32

   
   

   ∴  τ =	16T '
   	32

   
   But T ' = √M² + T²
   

   ∴  τ =	16T '	√M² + T²
   	πd3

---

54. A solid shaft of diameter d and length L is fixed at both the ends. A torque, T0 is applied at a distance, L/4 from the left end as shown in the figure given below.
    

1. 1. 16T0

      π d³

   
   
   

   2. 12T0

      π d³

   
   
   

   3. 8T0

      π d³

   
   
   

   4. 4T0

      π d³

   
   
   

---

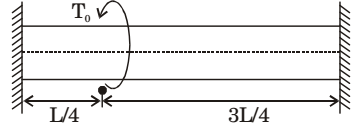
1. View Hint View Answer Discuss in Forum

   τmax =	16	[√M² + T²]
   	πd³

   
   But M = 0
   

   ∴  τmax =	16T0
   	πd³

   
   Alternately
   

   We know,	T	=	τ
   	J		r

   
   

   Where,   J =	πd4
   	32

   
   

   ∴  τ =	Tr	=	T0 × R × 32	=	16T0
   	J		πd4		πd3

   Correct Option: A

   τmax =	16	[√M² + T²]
   	πd³

   
   But M = 0
   

   ∴  τmax =	16T0
   	πd³

   
   Alternately
   

   We know,	T	=	τ
   	J		r

   
   

   Where,   J =	πd4
   	32

   
   

   ∴  τ =	Tr	=	T0 × R × 32	=	16T0
   	J		πd4		πd3

---

---

55. The maximum deflection of the beam is

1. 1. 24Pl³

      Ebt³

   
   
   

   2. 12Pl³

      Ebt³

   
   
   

   3. 8Pl³

      Ebt³

   
   
   

   4. 6Pl³

      Ebt³

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Maximum deflection of the beam
   

   ymax =	Pl³	=	6Pl³
   	3EI		Ebt³

   
   

   where,   I =	bt³
   	18l

   Correct Option: D

   Maximum deflection of the beam
   

   ymax =	Pl³	=	6Pl³
   	3EI		Ebt³

   
   

   where,   I =	bt³
   	18l

---