121. The state of stress at a point is given by σ_x = – 6 MPa, σ_y = 4 MPa, and τ_xy = – 8 MPa. The maximum tensile stress (in MPa) at the point is ______

1. 1. 8

   
   
   

   2. 8.43

   
   
   

   3. 43

   
   
   

   4. 3.4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   

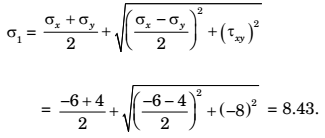
   Correct Option: B

   

---

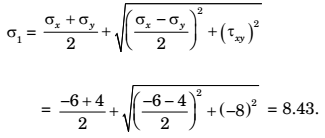
122. The state of plane-stress at a point is given by σ_x =200 MPa, σ_y =100 MPa and τ_xy = 100 MPa. The maximum shear stress

1. 1. 111.8

   
   
   

   2. 150.1

   
   
   

   3. 180.3

   
   
   

   4. 223.6

   
   
   

---

1. View Hint View Answer Discuss in Forum

   σ_x = 200MPa σ_y =100MPa z_xy =100MPa
   
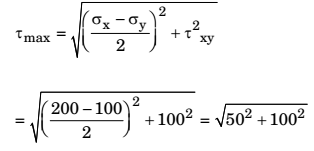
   = 111.80 MPa.

   Correct Option: A

   σ_x = 200MPa σ_y =100MPa z_xy =100MPa
   
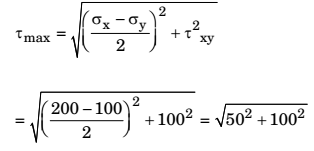
   = 111.80 MPa.

---

---

123. If the principal stresses in a plane stress problem are σ₁ = 100 MPa, σ₂ = 40 MPa, the magnitude of the maximum shear stress (in MPa) will be

1. 1. 60

   
   
   

   2. 50

   
   
   

   3. 30

   
   
   

   4. 20

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Maximum shear stress,
   

   τmax =	σ1 − σ2
   	2

   
   

   =	10 − 40	=	60	= 30 MPa
   	2		2

   Correct Option: C

   Maximum shear stress,
   

   τmax =	σ1 − σ2
   	2

   
   

   =	10 − 40	=	60	= 30 MPa
   	2		2

---

124. A shaft subjected to torsion experiences a pure shear stress x on the surface. The maximum principal stress on the surface which is at 45° to the axis will have a value

1. 1. τ cos 45°

   
   
   

   2. 2τ cos 45°

   
   
   

   3. τcos² 45°

   
   
   

   4. 2τ sin 45° cos 45°

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
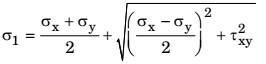
   σ_x = σ_y = 0, τ_zy = τ
   σ₁ = τ
   σ₁ = 2τ sin (45) cos (45) = τ

   Correct Option: D

   
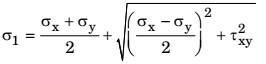
   σ_x = σ_y = 0, τ_zy = τ
   σ₁ = τ
   σ₁ = 2τ sin (45) cos (45) = τ

---

---

125. Below figure shows a rigid bar hinged at A and supported in a horizontal position by two vertical identical steel wires. Neglect the weight of the beam. The tension T₁ and T₂ induced in these wires by a vertical load P applied as shown are
     

1. 1. T1 = T2 =	P
      	2

   
   
   

   2. T1 =	Pal	, T2 =	Pbl
      	(a² + b²)		(a² + b²)

   
   
   

   3. T1 =	Pbl	, T2 =	Pal
      	(a² + b²)		(a² + b²)

   
   
   

   4. T1 =	Pal	, T2 =	Pal
      	2(a² + b²)		2(a² + b²)

   
   
   

---

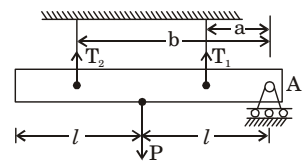
1. View Hint View Answer Discuss in Forum

   
   
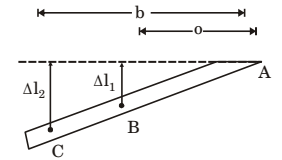
   Σy = O
   T₁ + T₂ – P – RA = O –(i)
   ΣM_A = O
   T₁ (a) + T₂ (b) = P (l) –(ii)
   Using similar Δ’s in fig (2)
   

   Δl1	=	Δl2	⇒		Δl1 =	T1L	Δl2 =	T2L
   a		b				AE		AE

   
   

   T1	=	T2
   a		b

   
   Putting above eqⁿ in eqⁿ (ii)
   

   T1(a) +	b2	T1 = P(l)
   	a

   
   

   T1 =	Pal	T2 =	Pbl
   	(a² + b²)		(a² + b²)

   Correct Option: B

   
   
   Σy = O
   T₁ + T₂ – P – RA = O –(i)
   ΣM_A = O
   T₁ (a) + T₂ (b) = P (l) –(ii)
   Using similar Δ’s in fig (2)
   

   Δl1	=	Δl2	⇒		Δl1 =	T1L	Δl2 =	T2L
   a		b				AE		AE

   
   

   T1	=	T2
   a		b

   
   Putting above eqⁿ in eqⁿ (ii)
   

   T1(a) +	b2	T1 = P(l)
   	a

   
   

   T1 =	Pal	T2 =	Pbl
   	(a² + b²)		(a² + b²)

---