61. In a simply-supported beam loaded as shown below, the maximum bending moment in Nm is
    
    

1. 1. 25

   
   
   

   2. 30

   
   
   

   3. 35

   
   
   

   4. 60

   
   
   

---

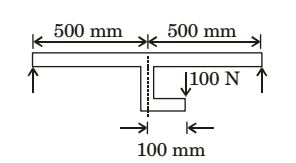
1. View Hint View Answer Discuss in Forum

   
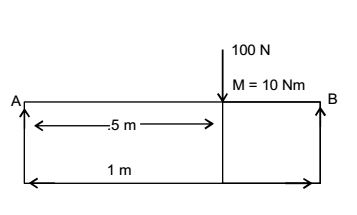
   Taking moment about A,
   100 × .5 + 10 = R_B
   R_B = 60 N
   ∴ R_A = 100 – 60 = 40N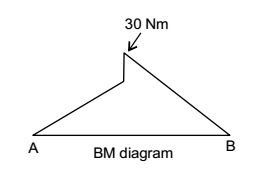
   

   Correct Option: B

   
   Taking moment about A,
   100 × .5 + 10 = R_B
   R_B = 60 N
   ∴ R_A = 100 – 60 = 40N
   

---

62. A free bar of length/ is uniformly heated from 0°C to a temperature t°C, α is the coefficient of linear expansion and E the modulus of elasticity. The stress in the bar is

1. 1. αtE

   
   
   

   2. αtE/2

   
   
   

   3. Zero

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For thermal stress to be developed there must be constraint in the system to oppose. So strain develops but there is no thermal stress.

   Correct Option: C

   For thermal stress to be developed there must be constraint in the system to oppose. So strain develops but there is no thermal stress.

---

---

63. Determine the temperature rise necessary to induce buckling in a 1 m long circular rod of diameter 40 mm shown in the figure below. Assume the rod to be pinned at its ends and the coefficient of thermal expansion as 20 × ^10–6/°C. Assume uniform heating of the bar.
    

1. 1. 49.35°C

   
   
   

   2. 48.51°C

   
   
   

   3. 59.35°C

   
   
   

   4. 48.25°C

   
   
   

---

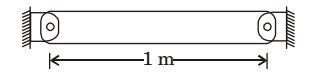
1. View Hint View Answer Discuss in Forum

   
   Let Bucking load be P
   δl = αΔTL
   

   ∴ ΔT =	δl	- (i)
   	αL

   
   We know:
   

   δl =	PL	⇒ =	AEδl	- (ii)
   	AE		L

   
   

   Pcolumn =	π²EI	- (iii)[Both ends hinged]
   	L²

   
   Compare equation (ii) + (iii)
   

   AE	δl	=	π²EI
   	L		L²

   
   

   Sl =	π²l	- (iv)
   	LA

   
   Putting the value of equation (iv) in equation (i)
   

   ΔT =	π²I		1		=	π²I
   	LA		αL			L²Aα

   
   

   ΔT =	π² ×	π	× (0.040)4
   		64
   	1³ ×	π	× (0.040)² × (20 × 10-6)
   		4

   
   ΔT = 49.35°C

   Correct Option: A

   
   Let Bucking load be P
   δl = αΔTL
   

   ∴ ΔT =	δl	- (i)
   	αL

   
   We know:
   

   δl =	PL	⇒ =	AEδl	- (ii)
   	AE		L

   
   

   Pcolumn =	π²EI	- (iii)[Both ends hinged]
   	L²

   
   Compare equation (ii) + (iii)
   

   AE	δl	=	π²EI
   	L		L²

   
   

   Sl =	π²l	- (iv)
   	LA

   
   Putting the value of equation (iv) in equation (i)
   

   ΔT =	π²I		1		=	π²I
   	LA		αL			L²Aα

   
   

   ΔT =	π² ×	π	× (0.040)4
   		64
   	1³ ×	π	× (0.040)² × (20 × 10-6)
   		4

   
   ΔT = 49.35°C

---

64. A frame of two arms of equal length L is shown in the adjacent figure. The flexural rigidity of each arm of the frame is El. The vertical deflection at the point of application of load P is
    

1. 1. PL3

      3EI

   
   
   

   2. 2PL3

      3EI

   
   
   

   3. PL3

      EI

   
   
   

   4. 4PL3

      3EI

   
   
   

---

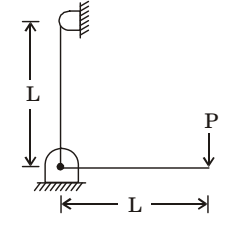
1. View Hint View Answer Discuss in Forum

   EI	d2y	= - Mx
   	dx2

   
   or M_x = – P (L–x)
   

   ∴ EI	d2y	= P (L–x)
   	dx2

   
   Integrating two times and
   puting x = L, we get
   

   y =	PL3
   	3EI

   
   

   U =	P2L3	+	P2L3	=	4P2L3
   	2EI		6EI		6EI

   
   

   ∴	1	× P × deflection =	4P2L3
   	2		6EI

   
   

   or Deflection =	4P2L3
   	6EI

   Correct Option: D

   EI	d2y	= - Mx
   	dx2

   
   or M_x = – P (L–x)
   

   ∴ EI	d2y	= P (L–x)
   	dx2

   
   Integrating two times and
   puting x = L, we get
   

   y =	PL3
   	3EI

   
   

   U =	P2L3	+	P2L3	=	4P2L3
   	2EI		6EI		6EI

   
   

   ∴	1	× P × deflection =	4P2L3
   	2		6EI

   
   

   or Deflection =	4P2L3
   	6EI

---

---

65. Two identical cantilever beams are supported as shown, with their free ends in contact through a rigid roller. After the load P is applied, the free ends will have
    

1. 1. equal deflections but not equal slopes

   
   
   

   2. equal slopes but not equal deflections

   
   
   

   3. equal slopes as well as equal deflections

   
   
   

   4. neither equal slopes nor equal deflections

   
   
   

---

1. View Hint View Answer Discuss in Forum

   As it is rigid roller deflection must be same because after deflection they also will be in contact but slope unequal.

   Correct Option: A

   As it is rigid roller deflection must be same because after deflection they also will be in contact but slope unequal.

---