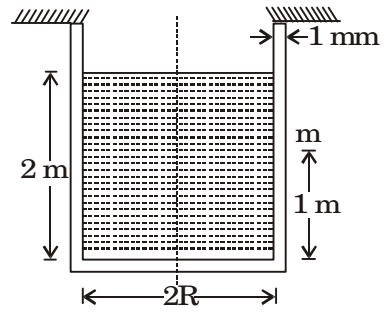
96. The axial and circumferential stress (σa, σc) experienced by the cylinder wall at mid-depth (m as shown) are

1. 1. (10,10) MPa

   
   
   

   2. (5,10) MPa

   
   
   

   3. (10,5)MPa

   
   
   

   4. (5, 5) MPa

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Pressure at mid – depth = ρgh = 10³ × 10 × 1 = 10⁴ N/m²
   

   ∴ σa =	pd	+	104 × 2
   	4t		4 × 10-3

   
   = 5 × 10⁶ N/mm² = 5 MPa
   

   σa =	pd	+	104 × 2	= 10MPa
   	2t		2 × 10-3

   Correct Option: B

   Pressure at mid – depth = ρgh = 10³ × 10 × 1 = 10⁴ N/m²
   

   ∴ σa =	pd	+	104 × 2
   	4t		4 × 10-3

   
   = 5 × 10⁶ N/mm² = 5 MPa
   

   σa =	pd	+	104 × 2	= 10MPa
   	2t		2 × 10-3

---

97. A rod of length L and diameter D is subjected to a tensile load P. Which of the following is sufficient to calculate the resulting change in diameter?

1. 1. Young's modulus

   
   
   

   2. Shear modulus

   
   
   

   3. Poisson's ratio

   
   
   

   4. Both Young's modulus and shear modulus

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Both Young's modulus and shear modulus

   Correct Option: D

   Both Young's modulus and shear modulus

---

---

98. A 200 × 100 × 50 mm steel block is subjected to a hydro static pressure of 15 MPa. The Young's modulus and Poisson's ratio of the material are 200 GPa and 0.3 respectively. The change in the volume of the block in mm³ is

1. 1. 85

   
   
   

   2. 90

   
   
   

   3. 100

   
   
   

   4. 110

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: B

   NA

---

99. In terms of Poisson's ratio (μ) the ratio of Young's modulus (E) to Shear modulus (G) of elastic materials is

1. 1. 2(1 + μ)

   
   
   

   2. 2 (1– μ)

   
   
   

   3. 	1	(1 + μ)
      	2

   
   
   

   4. 	1	(1 - μ)
      	2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   We know E = 2G[1 + v]
   E/G = 2[1 + v].
   
   18. Here, P_x = P_x = P_x = – 15 × 10⁶ Pa
   (compression)
   

   Now, ex	Px	=	Py	=	Pz	= 3 × 10-5
   	T2		2π		π

   
   where, m = Poisson’s ratio
   e_x = e_y = e_z = 3 × 10^-5
   e_x + e_y + e_z = 9 × 10^-5
   ∴ Change in volume = Total strain × Original = 90 m³

   Correct Option: A

   We know E = 2G[1 + v]
   E/G = 2[1 + v].
   
   18. Here, P_x = P_x = P_x = – 15 × 10⁶ Pa
   (compression)
   

   Now, ex	Px	=	Py	=	Pz	= 3 × 10-5
   	T2		2π		π

   
   where, m = Poisson’s ratio
   e_x = e_y = e_z = 3 × 10^-5
   e_x + e_y + e_z = 9 × 10^-5
   ∴ Change in volume = Total strain × Original = 90 m³

---

---

100. If the wire diameter of a compressive helical spring is increased by 2%, the change in spring stiffness (in%) is _______ (correct to two decimal places.)

1. 1. 8.243%

   
   
   

   2. 24%

   
   
   

   3. 3%

   
   
   

   4. 43%

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Stiffness of helical spring
   

   k =	Gd4
   	64R3 n

   
   ∴ k ∝ d⁴
   

   	k'	=		d'		4
   	k			d

   
   

   k' =		1.02 d		4	k
   		d

   
   k' = 1.08243 k
   

   % increase in k =	k' - k	× 100%
   	k

   
   

   =		1.08243 k - k		× 100% = 8.243%
   		k

   Correct Option: A

   Stiffness of helical spring
   

   k =	Gd4
   	64R3 n

   
   ∴ k ∝ d⁴
   

   	k'	=		d'		4
   	k			d

   
   

   k' =		1.02 d		4	k
   		d

   
   k' = 1.08243 k
   

   % increase in k =	k' - k	× 100%
   	k

   
   

   =		1.08243 k - k		× 100% = 8.243%
   		k

---