26. The beams, one having square cross-section and another circular cross-section, are subjected to the same amount of bending moment. If the cross sectional area as well as the material of both the beams are the same then
    

1. 1. maximum bending stress developed in both the beams is the same
      

   
   
   

   2. the circular beam experience more bending stress than the square one
      

   
   
   

   3. the square beam experiences more bending stress than the circular one
      

   
   
   

   4. as the material is same both beams will experience same deformation
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Since cross-sectional area of square and circular cross-sections are equal
   Let d = diameter of circular cross-section
   a² = side of square
   

   ∴	π	d2 = a2
   	4

   
   Now, σ for circular cross section
   

   =	M.C.
   	I

   
   
   
   

   =	M.	d	=	32M
   		2
   	M.	d2		πd3
   		64

   
   σ for square cross section
   

   =	M.C.	= M	(a / 2)	=	6M
   	I		(a4 / 12)		a3

   
   
   
   
   

   	σ for circular cross - section	=	32M
   			πd3
   	σ for circular cross - section		6M
   			d3

   
   

   =	32M	×	a3
   	πd3		6M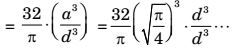

   
   
   

   Since , a =	π	d2 = 7
   	4

   
   σ for circular cross-section > σ for square cross section.

   Correct Option: B

   Since cross-sectional area of square and circular cross-sections are equal
   Let d = diameter of circular cross-section
   a² = side of square
   

   ∴	π	d2 = a2
   	4

   
   Now, σ for circular cross section
   

   =	M.C.
   	I

   
   
   
   

   =	M.	d	=	32M
   		2
   	M.	d2		πd3
   		64

   
   σ for square cross section
   

   =	M.C.	= M	(a / 2)	=	6M
   	I		(a4 / 12)		a3

   
   
   
   
   

   	σ for circular cross - section	=	32M
   			πd3
   	σ for circular cross - section		6M
   			d3

   
   

   =	32M	×	a3
   	πd3		6M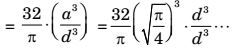

   
   
   

   Since , a =	π	d2 = 7
   	4

   
   σ for circular cross-section > σ for square cross section.

---

27. A cantilever beam has the square cross section of 10 mm × 10 mm. It carries a transverse load of 10 N. Considering only the bottom fibres of the beam, the correct representation of the longitudinal variation of the bending stress is
    
    
    

1. 1. 
      

   
   
   

   2. 
      

   
   
   

   3. 
      

   
   
   

   4. 
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Here , I =	bh3	=	0.01 × 0.013	m4
   	12		12

   
   y = 0.005 m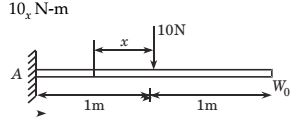
   
   At left extreme of cantilever
   σ_bending = 60 × 1 MPa = 60 MPa after 1 m
   σ_bending = 60 × 0 MPa = 0 MPa and it will continue over whole span.
   
   

   σ(bending stress) =	Mxy	=	(10x)(0.005)	N / m2
   	I		(0.01)4 / 12

   
   σ_bending = 60 x MPa (straight line equation)

   Correct Option: A

   Here , I =	bh3	=	0.01 × 0.013	m4
   	12		12

   
   y = 0.005 m
   
   At left extreme of cantilever
   σ_bending = 60 × 1 MPa = 60 MPa after 1 m
   σ_bending = 60 × 0 MPa = 0 MPa and it will continue over whole span.
   
   

   σ(bending stress) =	Mxy	=	(10x)(0.005)	N / m2
   	I		(0.01)4 / 12

   
   σ_bending = 60 x MPa (straight line equation)

---

---

28. A cyiindrical elastic body subjected to pure torsion about its axis develops
    

1. 1. tensile stress in a direction 45° to the axis
      

   
   
   

   2. no tensile or compressive stress
      

   
   
   

   3. maximum shear stress along the axis of the shaft
      

   
   
   

   4. maximum shear stress at 45° to the axis

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   Pure torsion σ_x = σ_y = 0, τ_xy = τ
   principle stress
   

   σ1 , 2 =	σx + σy	± √			σx - σy		²	+ τ²xy
   	2				2

   
   σ_{1 , 2} = ± τ_xy
   So, angle of maximum principle stress
   

   tan(2θp) =	2τxy	= ∞
   	σx - σy

   
   

   2θp =	π
   	2

   
   

   θp =	π	or 45°
   	4

   
   

   Correct Option: A

   
   Pure torsion σ_x = σ_y = 0, τ_xy = τ
   principle stress
   

   σ1 , 2 =	σx + σy	± √			σx - σy		²	+ τ²xy
   	2				2

   
   σ_{1 , 2} = ± τ_xy
   So, angle of maximum principle stress
   

   tan(2θp) =	2τxy	= ∞
   	σx - σy

   
   

   2θp =	π
   	2

   
   

   θp =	π	or 45°
   	4

   
   

---

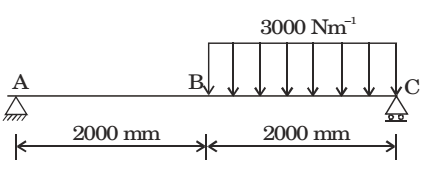
29. The maximum bending moment occurs at

1. 1. location B

   
   
   

   2. 2675 mm to the right of A

   
   
   

   3. 2500 mm to the right of A

   
   
   

   4. 3225 mm to the right of A

   
   
   

---

1. View Hint View Answer Discuss in Forum

   R_A = 1500 N
   R_B = 4500 N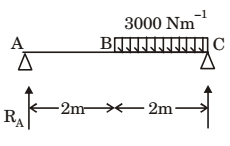
   
   SF = R_A –3000 (x–2)
   SF_x=2 = 1500 SF_x=4 = –4500
   SF = 1500 – 3000 (x–2) = 0 [For max BM]
   x = 2.5 m
   x = 2500 mm from A.

   Correct Option: C

   R_A = 1500 N
   R_B = 4500 N
   
   SF = R_A –3000 (x–2)
   SF_x=2 = 1500 SF_x=4 = –4500
   SF = 1500 – 3000 (x–2) = 0 [For max BM]
   x = 2.5 m
   x = 2500 mm from A.

---

---

30. A concentrated load P acts on a simply supported beam of span L at a distance L/3 from the left support. The bending moment at the point of application of the load is given by

1. 1. PL

      3

   
   
   

   2. 2PL

      3

   
   
   

   3. PL

      9

   
   
   

   4. 2PL

      9

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
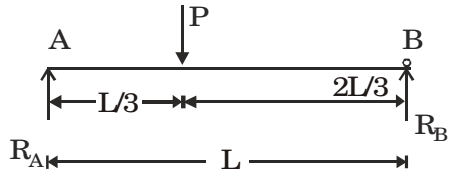
   R_A + R_B =P
   

   RA =	2P
   	3

   
   

   RB =	P
   	3

   
   BM_x = R_A x– P (x–L/3)
   

   BMx=L/3 = RA	L	- P		L	+	L		= RA	L
   	3			3		3			3

   
   

   BM =	2PL
   	9

   Correct Option: D

   
   R_A + R_B =P
   

   RA =	2P
   	3

   
   

   RB =	P
   	3

   
   BM_x = R_A x– P (x–L/3)
   

   BMx=L/3 = RA	L	- P		L	+	L		= RA	L
   	3			3		3			3

   
   

   BM =	2PL
   	9

---