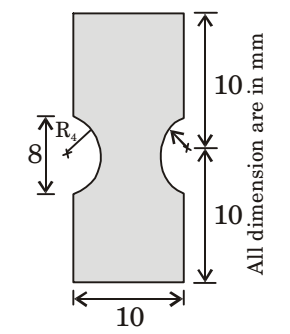
76. The figure shows cross-section of a beam subjected to bending. The area moment of inertia (in mm⁴) of this cross-section about its base is
    

1. 1. 21439.06 mm⁴

   
   
   

   2. 11439.06 mm⁴

   
   
   

   3. 31439.06 mm⁴

   
   
   

   4. 21439 mm⁴

   
   
   

---

1. View Hint View Answer Discuss in Forum

   I _base =I _{rect abt base} -2I _{semicircle abt base}
   I =((I_C.G +AY²) -2(I_C.G +AY²)
   

   =		bd3	+ (bd)y2		- 2		π		d2	+		1	× πr2y2
   		12					64		(2)			2

   
   

   =		10 × 203	+ 10 × 20 × 102		- 2		π	×	84	+	1	× π× 42 × 102
   		12					64		(2)		2

   
   = 21439.06 mm⁴.

   Correct Option: A

   I _base =I _{rect abt base} -2I _{semicircle abt base}
   I =((I_C.G +AY²) -2(I_C.G +AY²)
   

   =		bd3	+ (bd)y2		- 2		π		d2	+		1	× πr2y2
   		12					64		(2)			2

   
   

   =		10 × 203	+ 10 × 20 × 102		- 2		π	×	84	+	1	× π× 42 × 102
   		12					64		(2)		2

   
   = 21439.06 mm⁴.

---

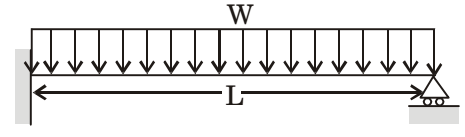
77. A beam of length L is carrying a uniformly distributed load w per unit length. The flexural rigidity of the beam is EI. The reaction at the simple support at the right end is
    

1. 1. wL

      2

   
   
   

   2. 3wL

      8

   
   
   

   3. wL

      4

   
   
   

   4. wL

      8

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   ∆_B = 0
   

   	WL4	-	RL3	= 0
   	8EI		3EI

   
   

   R =	3WL
   	8

   Correct Option: B

   
   ∆_B = 0
   

   	WL4	-	RL3	= 0
   	8EI		3EI

   
   

   R =	3WL
   	8

---

---

78. A simply supported beam of length 3L is subjected to the loading shown in the figure.
    
    It is given that P = 1 N, L = 1 m and Young's modulus E = 200 GPa. The cross-section is a square with dimension 10 mm × 10 mm. The bending stress (in Pa) at the point A located at the top surface of the beam at the distance of 1.5 L from the left end is _______.

1. 1. 0

   
   
   

   2. 1

   
   
   

   3. 2

   
   
   

   4. 3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   R_E = P/3N
   R_B = – P/3 N
   

   BMX=1.51 =	P	X - P(X - L)
   	3

   
   

   =	P		3L		- P		3L	- L		= 0
   	3		2				2

   
   BM = 0 0 = 0

   Correct Option: A

   
   R_E = P/3N
   R_B = – P/3 N
   

   BMX=1.51 =	P	X - P(X - L)
   	3

   
   

   =	P		3L		- P		3L	- L		= 0
   	3		2				2

   
   BM = 0 0 = 0

---

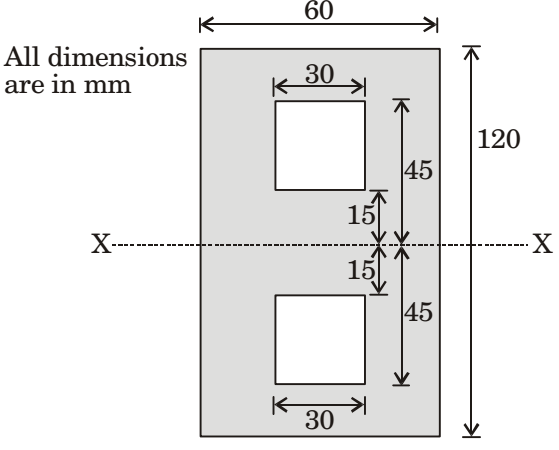
79. The value of moment of inertia of the section shown in the figure about the axis-XX is
    

1. 1. 8.5050 × 10⁶ mm⁴

   
   
   

   2. 6.8850 × 10⁶ mm⁴

   
   
   

   3. 7.7625 × 10⁶ mm⁴

   
   
   

   4. 8.5725 × 10⁶ mm⁴

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Moment of Inertia,
   

   Ixx =	1	[(120)3 × 60] - 2		1	× (30)4 + 30 × 30 × 30
   	12			12

   
   = 6.885 × 10⁶ mm⁴

   Correct Option: B

   Moment of Inertia,
   

   Ixx =	1	[(120)3 × 60] - 2		1	× (30)4 + 30 × 30 × 30
   	12			12

   
   = 6.885 × 10⁶ mm⁴

---

---

80. Consider a simply supported beam of length, 50h, with a rectangular cross-section of depth, h, and width, 2h. The beam carries a vertical point load, P, at its mid-point. The ratio of the maximum shear stress to the maximum bending stress in the beam is

1. 1. 0.02

   
   
   

   2. 0.10

   
   
   

   3. 0.05

   
   
   

   4. 0.01

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

   τmax =	0.75P	=	0.375P		Pmax =	P
   	h22		h2			2

   
   

   	τmax	=	0.375	= 0.01
   	σmax		37.5

   Correct Option: D

   
   

   τmax =	0.75P	=	0.375P		Pmax =	P
   	h22		h2			2

   
   

   	τmax	=	0.375	= 0.01
   	σmax		37.5

---