The state of stress at a point on an element is shown in

The state of stress at a point on an element is shown in figure (a). The same state of stress is shown in another coordinate system in figure (b).

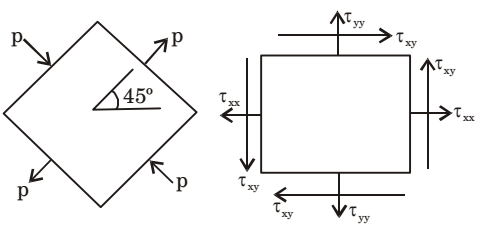
The components (τ_xx, τ_yy, τ_xy,) are given by

σ_θ =		σ_x + σ_y		+		σ_x - σ_y		cos2θ + τ_xysine2θ
		2				2

Here θ = - 45
σ_θ = T_xy
σ_x = p
σ_y = - p

σ_θ =T_xy =		P + P		+		P - P		cos90° = 0
		2				2

When θ = + 45

σ_θ =		P - P		+		P + P		cos90°
		2				2

When θ = 45° T_θ = T_xy

T_θ =		σ_x - σ_y		sin2θ - T_xy cos2θ
		2

T_θ = T_xy =		P + P		sin90° = P
		2

∴ T_xx, T_yy, T_xy = 0, 0, p

		p	, -	p	, 0
		√2		√2

		p, - p,	p
			√2

		0, 0,	p
			√2