-
Determine the temperature rise necessary to induce buckling in a 1 m long circular rod of diameter 40 mm shown in the figure below. Assume the rod to be pinned at its ends and the coefficient of thermal expansion as 20 × 10–6/°C. Assume uniform heating of the bar.
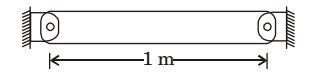
-
- 49.35°C
- 48.51°C
- 59.35°C
- 48.25°C
Correct Option: A

Let Bucking load be P
δl = αΔTL
| ∴ ΔT = | - (i) | |
| αL |
We know:
| δl = | ⇒ = | - (ii) | ||
| AE | L |
| Pcolumn = | - (iii)[Both ends hinged] | |
| L² |
Compare equation (ii) + (iii)
| AE | = | ||
| L | L² |
| Sl = | - (iv) | |
| LA |
Putting the value of equation (iv) in equation (i)
| ΔT = |  |  | = | |||
| LA | αL | L²Aα |
| ΔT = | π² × | × (0.040)4 | |
| 64 | |||
| 1³ × | × (0.040)² × (20 × 10-6) | ||
| 4 | |||
ΔT = 49.35°C

