106. An amplifier has an open-loop gain of 100, and its lower and upper-cut -off frequency of 100 Hz and 100 kHz, respectively. A feedback network with a feedback factor of 0.99 is connected to the amplifier. The new lower and upper-cut-off frequencies are at___and ___

1. 1. f_H = 10 MHz, f_L = 1 Hz

   
   
   

   2. f_H = 25 MHz, f_L = 10 Hz

   
   
   

   3. f_H = 100 MHz, f_L = 100 Hz

   
   
   

   4. f_H =10 MHz, f_L = 10 Hz

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Af =	A	=	100	= 1
   	1 + Aβ		1 + 100 × 0·99

   
   f^*_H = f_H. (1 + Aβ) = 100 × 10³ (1 + 0.99 × 100)
   = 10 MHz
   

   f*L =	fL	=	100	= 1 = 1 Hz.
   	1 + Aβ		(1 + 100 × 0·99)

   Correct Option: A

   Af =	A	=	100	= 1
   	1 + Aβ		1 + 100 × 0·99

   
   f^*_H = f_H. (1 + Aβ) = 100 × 10³ (1 + 0.99 × 100)
   = 10 MHz
   

   f*L =	fL	=	100	= 1 = 1 Hz.
   	1 + Aβ		(1 + 100 × 0·99)

---

107. A power amplifier delivers 50 W output at 50% efficiency. The ambient temperature is 25° C. If the maximum allowable junction temperature is 150° C, then the maximum thermal resistance Q_jc that can be tolerated is:

1. 1. 25° C/W

   
   
   

   2. 20° C/W

   
   
   

   3. 5° C/W

   
   
   

   4. 1° C/W

   
   
   

---

1. View Hint View Answer Discuss in Forum

   P_D = P₀ × efficiency
   = dissipated power at the output
   

   PD =	50 × 50	= 25 W
   	100

   
   Given that, T_i = 150° C
   T_A = 25°C
   Now,
   

   PD =	Ti – TA
   	Qjc

   
   where, T_i = instantaneous temperature
   T_A = ambient temp.
   

   Qjc =	Ti – TA	=	150 – 25	= 5° C/W
   	PD		25

   
   Q_jc = thermal resistance

   Correct Option: C

   P_D = P₀ × efficiency
   = dissipated power at the output
   

   PD =	50 × 50	= 25 W
   	100

   
   Given that, T_i = 150° C
   T_A = 25°C
   Now,
   

   PD =	Ti – TA
   	Qjc

   
   where, T_i = instantaneous temperature
   T_A = ambient temp.
   

   Qjc =	Ti – TA	=	150 – 25	= 5° C/W
   	PD		25

   
   Q_jc = thermal resistance

---

---

108. An R–C coupled amplifier is assumed to have a singlepole low frequency transfer function. The Maximum lower-cut -off frequency allowed for the amplifier to pass 50 Hz square wave with no more than 100% till is:

1. 1. 1 kHz

   
   
   

   2. 1 Hz

   
   
   

   3. 1.59 Hz

   
   
   

   4. 1.59 kHz

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Fractional tilt =	πfL
   	f

   
   where, f_L = Lower cut-off frequency
   f = applied signal frequency
   

   or fL =	f × fractional tilt
   	π

   
   

   or fL =	50 × 10/100
   	3·14

   
   = 1.59 Hz

   Correct Option: C

   Fractional tilt =	πfL
   	f

   
   where, f_L = Lower cut-off frequency
   f = applied signal frequency
   

   or fL =	f × fractional tilt
   	π

   
   

   or fL =	50 × 10/100
   	3·14

   
   = 1.59 Hz

---

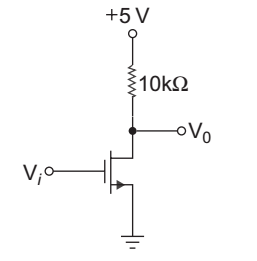
109. For the circuit shown below the transistor parameter are V_TN = 0.8 V and kn = 30 µ A/V². If output voltage is V₀ = 0.1 V, when input voltage is V_i = 4.2 V, the required transistor width-to-length ratio is:
     
     
     

1. 1. 1.568

   
   
   

   2. 1.982

   
   
   

   3. 0.731

   
   
   

   4. 2.825

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given that
   V_TN = 0.8 V
   k′_n = 30 µA/V²
   V₀ = 0.1 V
   V_i = 4.2 V
   From fig. V_GS = V_i = 4.2 V
   

   and ID =	5 – V0	=	5 – 0·1
   	10 kΩ		10 × 103

   
   

   =	4·9	= 0.49 mA
   	10 × 103

   
   

   Again ID =	1	. k'n		W			(VGS–VTN)2
   	2			L

   
   = 0.49 × 10^–3 or 0.49 × 10^–3
   

   =	1	× 30 × 10–6.		W			. (4.2 – 0.8)2
   	2			L

   
   

   or		W		=	0·49 × 103	= 2.825
   		L			15 × (3·4)2

   
   Hence alternative (D) is the correct choice.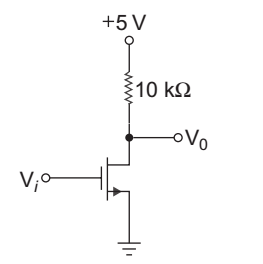

   
   

   Correct Option: D

   Given that
   V_TN = 0.8 V
   k′_n = 30 µA/V²
   V₀ = 0.1 V
   V_i = 4.2 V
   From fig. V_GS = V_i = 4.2 V
   

   and ID =	5 – V0	=	5 – 0·1
   	10 kΩ		10 × 103

   
   

   =	4·9	= 0.49 mA
   	10 × 103

   
   

   Again ID =	1	. k'n		W			(VGS–VTN)2
   	2			L

   
   = 0.49 × 10^–3 or 0.49 × 10^–3
   

   =	1	× 30 × 10–6.		W			. (4.2 – 0.8)2
   	2			L

   
   

   or		W		=	0·49 × 103	= 2.825
   		L			15 × (3·4)2

   
   Hence alternative (D) is the correct choice.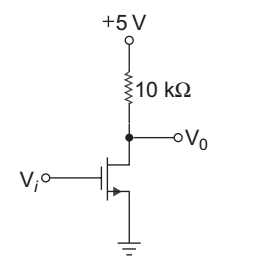

   
   

---

---

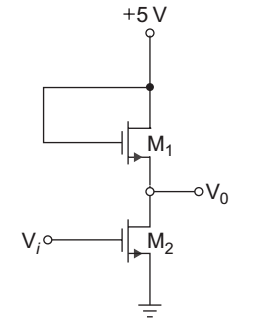
110. The transistors in the circuit of given below have parameter V_TN = 0.8 V, k_n = 40 µA/V² and λ = 0. The width-to-length ratio of M₂ is
     

     	W			= 1.
     	L		2

     
     If V₀ = 0.10 V when V_i = 5 V, then
     

     	W			for M1 is:
     	L		1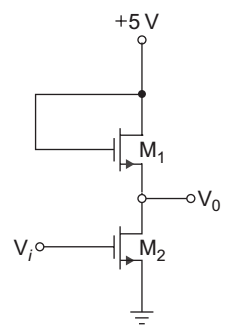

     
     
     

1. 1. 47.5

   
   
   

   2. 28.4

   
   
   

   3. 40.5

   
   
   

   4. 20.3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given that
   V_TN = 0.84
   k′_n = 40 µA/V²
   

   		W			= 1
   		L		2

   
   V₀ = 0.10 V
   V_i = 5 V
   For transistor M₂
   V_DS = 0.1 V
   V_GS1 = V_i = 5 V
   ∴ V_DS < V_GS – V_TN, therefore the transistor M₂ work in the linear region
   I_D2 = I_D1 = I_D
   

   ID2 =	1	k'n		W			. [2(VGS2 – VTn)VDS2 – V2DS2 ]…(A)
   	2			L		2

   
   

   ID1 =	1	kn′		W			(VGS1 – VTn)2 …(B)
   	2			L		1

   
   solving equation (A) and (B)
   

   1. (5 – 0.1 – 0.8)2 =		W			[2 . (5 – 0.8) 0.1 – (0.1)2]
   		L		1

   
   

   (4.1)2 =		W			[0·84 – 0.01]
   		L		1

   
   

   or =		W			=	(4.1)2	= 20.25
   		L		1		0·83

   
   Hence alternative (D) is the correct choice.

   
   

   Correct Option: D

   Given that
   V_TN = 0.84
   k′_n = 40 µA/V²
   

   		W			= 1
   		L		2

   
   V₀ = 0.10 V
   V_i = 5 V
   For transistor M₂
   V_DS = 0.1 V
   V_GS1 = V_i = 5 V
   ∴ V_DS < V_GS – V_TN, therefore the transistor M₂ work in the linear region
   I_D2 = I_D1 = I_D
   

   ID2 =	1	k'n		W			. [2(VGS2 – VTn)VDS2 – V2DS2 ]…(A)
   	2			L		2

   
   

   ID1 =	1	kn′		W			(VGS1 – VTn)2 …(B)
   	2			L		1

   
   solving equation (A) and (B)
   

   1. (5 – 0.1 – 0.8)2 =		W			[2 . (5 – 0.8) 0.1 – (0.1)2]
   		L		1

   
   

   (4.1)2 =		W			[0·84 – 0.01]
   		L		1

   
   

   or =		W			=	(4.1)2	= 20.25
   		L		1		0·83

   
   Hence alternative (D) is the correct choice.

   
   

---