Number System
- A number divided by 13 leaves a remainder 1 and if the quotient, thus obtained, is divided by 5, we get a remainder of 3. What will be the remainder if the number is divided by 65 ?
-
View Hint View Answer Discuss in Forum
Let the least number be x.
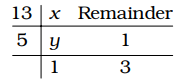
Correct Option: D
Let the least number be x.
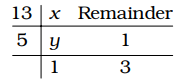
y = 5 × 1 + 3 = 8
x = 13 × 8 + 1 = 105
On dividing 105 by 65,
⇒ 105 = ( 65 × 1 ) + 40
Hence required remainder = 40
- In a question on division, the divisor is 7 times the quotient and 3 times the remainder. If the remainder is 28, then the dividend is
-
View Hint View Answer Discuss in Forum
Given , Remainder = 28
Let the quotient be Q and the remainder be R. Then
According to question ,
Divisor = 7 Q = 3 RCorrect Option: D
Given , Remainder = 28
Let the quotient be Q and the remainder be R. Then
According to question ,
Divisor = 7 Q = 3 R∴ Q = 3 R = 3 × 28 = 12 7 7
⇒ Quotient = 12
∴ Divisor = 7 Q = 7 × 12 = 84
∴ Dividend = Divisor × Quotient + Remainder = 84 × 12 + 28 = 1008 + 28 = 1036
Hence the dividend is 1036.
- A number consists of two digits. If the number formed by interchanging the digits is added to the original number, the resulting number (i.e. the sum) must be divisible by
-
View Hint View Answer Discuss in Forum
Let the number be 10a + b .
After interchanging the digits, the number obtained = 10b + a.Correct Option: A
Let the number be 10a + b .
After interchanging the digits, the number obtained = 10b + a.
According to the question,
Resulting number = 10a + b + 10b + a
Resulting number = 11a + 11b
Resulting number = 11 (a + b)
which is exactly divisible by 11.
- If two numbers are each divided by the same divisor, the remainders are respectively 3 and 4. If the sum of the two numbers be divided by the same divisor, the remainder is 2. The divisor is
-
View Hint View Answer Discuss in Forum
Let two numbers are a and b and the divisor is d .
According to question ,∴ R1 = a = 3 d ∴ R2 = b = 4 d
Correct Option: C
Let two numbers are a and b and the divisor is d .
According to question ,∴ R1 = a = 3 d ∴ R2 = b = 4 d Now , R = 3 + 4 = 3 + 4 = 2 d d
⇒ 7 - 2 = 5 is divisible by d .
Required divisor = 5 { ∴ d > 4 }
- (719 + 2) is divided by 6, the remainder is :
-
View Hint View Answer Discuss in Forum
Using the Binomial expansion , we have
(x + 1)n = xn + nc1 xn–1 +
nc2 xn– 2 + ..... + ncn–1 x +1
Here, each term except the last term contains x. Obviously, each term except the last term is exactly divisible by x.Correct Option: B
Using the Binomial expansion , we have
(x + 1)n = xn + nc1 xn–1 +
nc2 xn– 2 + ..... + ncn–1 x +1
Here, each term except the last term contains x. Obviously, each term except the last term is exactly divisible by x.
Following the same logic,
∴ 719 = (6 + 1)19 has each term except last term divisible by 6.
Hence, 719 + 2 when divided by 6 leaves remainder
⇒ 719 + 2 = 1 + 2 = 3
Hence the remainder is 3.

