Number System
- A number when divided by 6 leaves remainder 3. When the square of the same number is divided by 6, the remainder is :
-
View Hint View Answer Discuss in Forum
According to question ,
The remainder will be same. On dividing 9 by 6, remainder = 3
∴ ( Number )2 = 92 = 81Correct Option: D
According to question ,
The remainder will be same. On dividing 9 by 6, remainder = 3
∴ ( Number )2 = 92 = 81
On dividing 81 by 6
⇒ 81 = ( 6 × 13 ) + 3
Hence , Required remainder = 3
- A number divided by 13 leaves a remainder 1 and if the quotient, thus obtained, is divided by 5, we get a remainder of 3. What will be the remainder if the number is divided by 65 ?
-
View Hint View Answer Discuss in Forum
Let the least number be x.
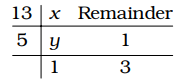
Correct Option: D
Let the least number be x.
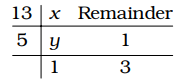
y = 5 × 1 + 3 = 8
x = 13 × 8 + 1 = 105
On dividing 105 by 65,
⇒ 105 = ( 65 × 1 ) + 40
Hence required remainder = 40
- When a number is divided by 893, the remainder is 193. What will be the remainder when it is divided by 47 ?
-
View Hint View Answer Discuss in Forum
As per the given above question ,
Here, 893 is exactly divisible by 47.
Hence, the required remainder is obtained on dividing 193 by 47.Correct Option: B
As per the given above question ,
Here, 893 is exactly divisible by 47.
Hence, the required remainder is obtained on dividing 193 by 47.
⇒ 193 = ( 47 × 4 ) + 5
∴ Remainder = 5
- Which of the following number is NOT divisible by 18 ?
-
View Hint View Answer Discuss in Forum
As we know that A number will be exactly divisible by 18 if it is divisible by 2 and 9 both. Clearly option ( d ) , 65043 is not divisible by 2.
Correct Option: D
As we know that A number will be exactly divisible by 18 if it is divisible by 2 and 9 both. Clearly option ( d ) , 65043 is not divisible by 2.
∴ Required number = 65043
- A number divided by 68 gives the quotient 269 and remainder zero. If the same number is divided by 67, the remainder is :
-
View Hint View Answer Discuss in Forum
According to question ,
Number = 269 × 68 + 0
Number = 269 × (67 + 1)Correct Option: B
According to question ,
Number = 269 × 68 + 0
Number = 269 × (67 + 1)
Number = 269 × 67 + 269
Clearly, remainder is obtained on dividing 269 by 67 that is 1.
Thus , required remainder is 1.

