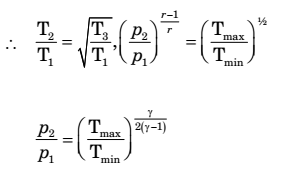Thermodynamics Miscellaneous
Direction: Consider a steam power plant using a reheat cycle as shown. Steam leaves the boiler and enters the turbine at 4 MPa, 350°C (h3 = 3095 kJ/kg). After expansion in the turbine to 400 kPa (h4 = 2609 kJ/kg), the steam is reheated to 350°C (h5 = 3170 kJ/kg), and then expanded in a low pressure turbine to 10 kPa (h6 = 2165 kJ/kg) the specific volume of liquid handled by the pump can be assumed to be 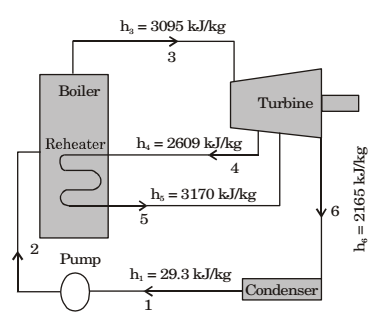
- The thermal efficiency of the plant neglecting pump work is
-
View Hint View Answer Discuss in Forum
Given: h1 = 29.3 kJ/kg
h2 =?
h3 = 3095 kJ/kg
h4 = 2609 kJ/kg
h5 = 3170 kJ/kg
h6 = 2165 kJ/kg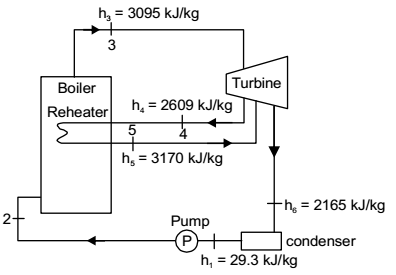
Turbine work
WT = (h3 – h4) + (h5 – h6)
= (3095 – 2609) + (3170 – 2165) =
1491 kJ/kg
Q = Heat input = (h3 – h1) + (h5 – h4)
= (3095 – 29.3) + 3(3170 – 2609) = 3626.7 kJ/kg
∴ Thermal efficiency of the plant= 1491 = 41.11% 3226.7 Correct Option: B
Given: h1 = 29.3 kJ/kg
h2 =?
h3 = 3095 kJ/kg
h4 = 2609 kJ/kg
h5 = 3170 kJ/kg
h6 = 2165 kJ/kg
Turbine work
WT = (h3 – h4) + (h5 – h6)
= (3095 – 2609) + (3170 – 2165) =
1491 kJ/kg
Q = Heat input = (h3 – h1) + (h5 – h4)
= (3095 – 29.3) + 3(3170 – 2609) = 3626.7 kJ/kg
∴ Thermal efficiency of the plant= 1491 = 41.11% 3226.7
- The compression ratio of a gas power plant cycle corresponding to maximum work output for the given temperature limits of Tmin and Tmax will be
-
View Hint View Answer Discuss in Forum
W = Turbine work – compressor work
W = Cp [(T3 – T4) – (T2 – T1)]Let T3 = t and T2 = T3 = C T1 T4 T4 W = CpT1 
t 
1 – 1 
- (C - 1) 
C
For maximum work output
dW = CpT1 
T 
1 
- 1 
= 0 dc C2
gives C2 = √t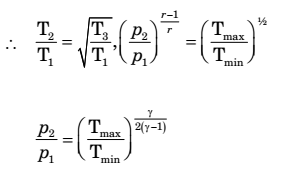
Correct Option: A
W = Turbine work – compressor work
W = Cp [(T3 – T4) – (T2 – T1)]Let T3 = t and T2 = T3 = C T1 T4 T4 W = CpT1 
t 
1 – 1 
- (C - 1) 
C
For maximum work output
dW = CpT1 
T 
1 
- 1 
= 0 dc C2
gives C2 = √t