141. If V_N and α are the nozzle exit velocity and nozzle angle in an impulse turbine, the optimum blade velocity is given by
     

1. 1. V_N cos 2α

   
   
   

   2. V_N sin 2α

   
   
   

   3. VN cos			α
      			2

   
   
   

   4. 	VN cos α
      	2

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: D

   NA

---

142. The following data pertain to a single stage impulse steam turbine: Nozzle angle = 20° Blade velocity = 200 m/s Relative steam velocity at entry = 350 m/s Blade inlet angle = 30° Blade exit angle = 25° If blade friction is neglected the work done per kg steam is

1. 1. 124 kJ

   
   
   

   2. 164 kJ

   
   
   

   3. 169 kJ

   
   
   

   4. 174 kJ

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
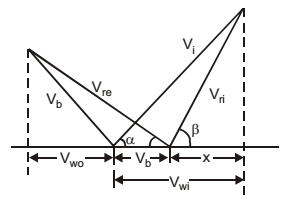
   Given :α = 20°
   β = 30°
   x = 350 cos 30° = 303 m/s
   ∴ V_wi = 303 + V_b
   = 303 + 200 = 503 m/s
   

   cos 25° =	200 + Vwo	= 0.9063
   	350

   
   V_wo =118 m/s
   Work done/kg of steam
   

   =	(Vwi + Vwo) Vb	kJ
   	1000

   
   

   =	(503 + 118) 200	= 124 kJ
   	1000

   
   

   Correct Option: A

   
   Given :α = 20°
   β = 30°
   x = 350 cos 30° = 303 m/s
   ∴ V_wi = 303 + V_b
   = 303 + 200 = 503 m/s
   

   cos 25° =	200 + Vwo	= 0.9063
   	350

   
   V_wo =118 m/s
   Work done/kg of steam
   

   =	(Vwi + Vwo) Vb	kJ
   	1000

   
   

   =	(503 + 118) 200	= 124 kJ
   	1000

   
   

---

---

143. A steam power plant has the boiler efficiency of 92%, turbine efficiency (mechanical) of 94%, generator efficiency of 95% and cycle efficiency of 44%. If 6% of the generated power is used to run the auxiliaries, the overall plant efficiency is

1. 1. 34%

   
   
   

   2. 39%

   
   
   

   3. 45%

   
   
   

   4. 30%

   
   
   

---

1. View Hint View Answer Discuss in Forum

   η₀ = η_b × η_m × η_s × η_c | 1 - η_a)
   = 0.92 × 0.94 × 0.95 × 0.44r × (1 – 0.06)
   η₀ = 34%

   Correct Option: A

   η₀ = η_b × η_m × η_s × η_c | 1 - η_a)
   = 0.92 × 0.94 × 0.95 × 0.44r × (1 – 0.06)
   η₀ = 34%

---

144. For a simple compressible system, v, s, p and T are specific volume, specific entropy, pressure and temperature, respectively. As per Maxwell’s relation,			δV			p is equal to
     			δS

1. 1. 			δp			t
      			δv

   
   
   

   2. 			δT			s
      			δp

   
   
   

   3. 			δs			t
      			δT

   
   
   

   4. -			δT			t
      			δv

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   dH = TdS + vdP
   

   ⇒			δT		S =			δV		P
   			δP					δS

   
   

   So, ⇒			δV		P =			δT		S
   			δS					δP

   
   

   Correct Option: B

   dH = TdS + vdP
   

   ⇒			δT		S =			δV		P
   			δP					δS

   
   

   So, ⇒			δV		P =			δT		S
   			δS					δP

   
   

---

---

145. If one mole of H₂ gas occupies a rigid container wi t h a capaci t y of 1000 l i t er s and t he temperature is raised from 27°C to 37°C, the change in pressure of the contained gas (round off to two decimal places), assuming ideal gas behavior, is _____ Pa. (R = 8.314 J/mol.K).
     

1. 1. 83.14 Pascal

   
   
   

   2. 82.14 Pascal

   
   
   

   3. 81.14 Pascal

   
   
   

   4. 84.14 Pascal

   
   
   

---

1. View Hint View Answer Discuss in Forum

   P₁ V = nRT₁
   P₂ V = nRT₁
   Now, Changs in pressure,
   P₂ – P₁ = nR (T₂ - T₁)
   ⇒ ∆P × 1 = 1 × 8.314(37 – 27)
   ⇒ ∆P = 83.14 Pascal

   Correct Option: A

   P₁ V = nRT₁
   P₂ V = nRT₁
   Now, Changs in pressure,
   P₂ – P₁ = nR (T₂ - T₁)
   ⇒ ∆P × 1 = 1 × 8.314(37 – 27)
   ⇒ ∆P = 83.14 Pascal

---