Thermodynamics Miscellaneous Easy Questions and Answers

Thermodynamics Miscellaneous

An ideal Brayton cycle, operating between the pressure limits of 1 bar and 6 bar, has minimum and maximum temperatures of 300 K and 1500 K. The ratio of specific heats of the working fluid is 1.4. The approximate final temperature in Kelvin at the end of the compression and expansion processes are respectively

1. 500 and 900
1. 900 and 500
1. 500 and 5400
1. 900 and 900

View Hint View Answer Discuss in Forum

Ideal Brayton cycle,

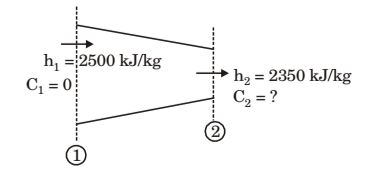
At the end of compression,
Temperature, T₂ = T₁ P₃ ^{γ - 1 /_γ}
T₄

= 300 × 6^0.4/_1.4 = 500 K
At the end of expansion;
Temperature, T₄ = T₃
P₃ ^γ-1/_γ
P₄

= 1500
6^0.4/_1.4

= 900K

Correct Option: A

Ideal Brayton cycle,

At the end of compression,
Temperature, T₂ = T₁ P₃ ^{γ - 1 /_γ}
T₄

= 300 × 6^0.4/_1.4 = 500 K
At the end of expansion;
Temperature, T₄ = T₃
P₃ ^γ-1/_γ
P₄

= 1500
6^0.4/_1.4

= 900K

The values of enthalpy of steam at the inlet and outlet of a steam turbine in a Rankine cycle are 2800 kJ/kg and 1800 kJ/kg respectively. Neglecting pump work, the specific steam consumption in kg/kW hour is

1. 3.60
1. 0.36
1. 0.06
1. 0.01

View Hint View Answer Discuss in Forum

41. Work done by the turbine
W = 2800 – 1800 = 1000 kJ/kg
= 1000 kW-s/kg
Specific fuel consumption = 1 × 3600
1000

= 3.6 kg/kW – hr

Correct Option: A

41. Work done by the turbine
W = 2800 – 1800 = 1000 kJ/kg
= 1000 kW-s/kg
Specific fuel consumption = 1 × 3600
1000

= 3.6 kg/kW – hr

Direction: The inlet and the outlet conditions of steam for an adiabatic steam turbine are as indicated in the notations are as usually followed.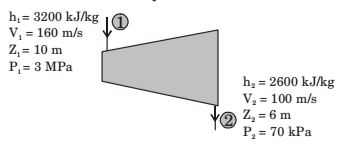

Assume the above turbine to be part of a simple Rankine cycle. The density of water at the inlet to the pump is 1000 kg/m3. Ignoring kinetic and potential energy effects, the specific work (in kJ/kg) supplied to the pump is

1. 0.293
1. 0.351
1. 2.930
1. 3.510

View Hint View Answer Discuss in Forum

Pump work
h_inlet + q = h_outlet + W_pump
here, q = 0
W_pump = h_inlet – h_outlet
∴ W = ∆h_pump
Reversible adiabatic
dq = dh– Vdp
∴ dh = Vdp
∴ d_hpump =V(p₂ – p₁) = 1/ρ (3000–70) kPa = 2.930kPa

Correct Option: C

Pump work
h_inlet + q = h_outlet + W_pump
here, q = 0
W_pump = h_inlet – h_outlet
∴ W = ∆h_pump
Reversible adiabatic
dq = dh– Vdp
∴ dh = Vdp
∴ d_hpump =V(p₂ – p₁) = 1/ρ (3000–70) kPa = 2.930kPa

If mass flow rate of steam through the turbine is 20 kg/s, the power output of the turbine (in MW) is

1. 12.157
1. 12.941
1. 168.001
1. 168.785

View Hint View Answer Discuss in Forum

SFEE h₁ + z₁g + c²₁ + Q = h₂ + z₂g + c²₂ + W
2 2

For adiabatic process, Q = 0
∴ h₂ + z₁g + c²₁ = h₂ + z₂g + c²₂ + W
2 2

Or 3200 × 10³ + 10 × 9.81 + 160 × 160
2

= 2600 × 10³ + 6 × 9.81 + 100 × 100 + W
2

⇒ W = 600 × 10³ + 39.24 + 2600 - 1000 + W
2

= 607839.24 × 20 J/s = 12.156 MW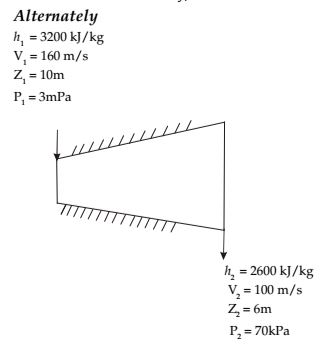

Applying S.F.E.E
w₁ h₁ + V²₁ + gz₁ + dQ w₂ h₂ + V²₂ + gz₂ + δw
2 dτ 2 dτ

Here, w₁ = mass flow rate
dQ = 0 for insulated turbine
dτ

∴ 20 3200 + 160² × 9.81 × 10
2 × 10³

= 20 2600 + 160² + 9.81 × 6 + dw
2 × 10³ 10³ dτ

Or dw = 20 (3200 - 2600) + 1 160² - 100² + 9.81(10 - 6)
dτ 10³ 2 2 10³

= 20 × {600 + 7.8 + 0.03924}
= 20 × 607.83924 kW
= 12156.7848 kW ≃ 12.157MW

Correct Option: A

SFEE h₁ + z₁g + c²₁ + Q = h₂ + z₂g + c²₂ + W
2 2

For adiabatic process, Q = 0
∴ h₂ + z₁g + c²₁ = h₂ + z₂g + c²₂ + W
2 2

Or 3200 × 10³ + 10 × 9.81 + 160 × 160
2

= 2600 × 10³ + 6 × 9.81 + 100 × 100 + W
2

⇒ W = 600 × 10³ + 39.24 + 2600 - 1000 + W
2

= 607839.24 × 20 J/s = 12.156 MW

Applying S.F.E.E
w₁ h₁ + V²₁ + gz₁ + dQ w₂ h₂ + V²₂ + gz₂ + δw
2 dτ 2 dτ

Here, w₁ = mass flow rate
dQ = 0 for insulated turbine
dτ

∴ 20 3200 + 160² × 9.81 × 10
2 × 10³

= 20 2600 + 160² + 9.81 × 6 + dw
2 × 10³ 10³ dτ

Or dw = 20 (3200 - 2600) + 1 160² - 100² + 9.81(10 - 6)
dτ 10³ 2 2 10³

= 20 × {600 + 7.8 + 0.03924}
= 20 × 607.83924 kW
= 12156.7848 kW ≃ 12.157MW

A compressor undergoes a reversible, steady flow process. The gas at inlet and outlet of the compressor is designated as state 1 and state 2 respectively. Potential and kinetic energy changes are to be ignored. The following notations are used: v = specific volume and P = pressure of the gas. The specific work required to be supplied to the compressor for this gas compression process is

1. ∫²₁ Pdv
1. ∫²₁vdP
1. v₁ (P₂–P₁)
1. –P₂ (v₁– v₂)

View Hint View Answer Discuss in Forum

h = u + Pv
⇒ dh =du + Pdv + vdP
But dQ =du + Pdv
∴ du = dQ –Pdv
∴ dh = dQ – Pdv + Pdv + vdP
⇒ dh = dQ + vdP
⇒ –vdP = d(P.E) + d(K.E) + dW
Since K.E and P.E are constant
∴ dW = ∫²₁vdP

Correct Option: B

h = u + Pv
⇒ dh =du + Pdv + vdP
But dQ =du + Pdv
∴ du = dQ –Pdv
∴ dh = dQ – Pdv + Pdv + vdP
⇒ dh = dQ + vdP
⇒ –vdP = d(P.E) + d(K.E) + dW
Since K.E and P.E are constant
∴ dW = ∫²₁vdP

Temperature, T₂ = T₁		P₃		^{γ - 1 /_γ}
		T₄

Temperature, T₄ =	T₃

	P₃	^γ-1/_γ
	P₄

=	1500
	6^0.4/_1.4

Temperature, T₂ = T₁		P₃		^{γ - 1 /_γ}
		T₄

Thermodynamics Miscellaneous

Thermodynamics Miscellaneous

Thermodynamics

Correct Option: A

Correct Option: A

Correct Option: C

Correct Option: A

Correct Option: B