Thermodynamics Miscellaneous Easy Questions and Answers

Thermodynamics Miscellaneous

In an air-standard Otto cycle, the compression ratio is 10. The condition at the beginning of the compression process is 100 kPa and 27°C. Heat added at constant volume is 1500 kJ/kg, while 700 kJ/kg of heat is rejected during the other constant volume process in the cycle. Specific gas constant for air = 0.287 kJ/kgK. The mean effective pressure (in kPa) of the cycle is

1. 103
1. 310
1. 515
1. 1032

View Hint View Answer Discuss in Forum

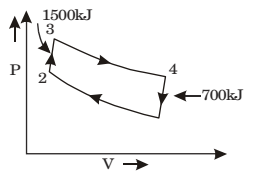
Here, P₁ = 100 kPa
T₁ = 27°C
V₄ = V₁ = 10
V₃ V₂

C_v = 0.287 kJ/kgK
P_m × (V₁ – V₂ )= work done
= h₁ – h₂
= 1500 – 700 = 800 kJ
Now P₁V₁ = mRT₁
or 100 × 10³ × V₁ = 1× 0.287 × 10³ × 300
or V₁ = 0.861
∴ V₂ = 0.0861
Now P_m (0.861 – 0.0861) = 800
∴ P_m = 1032 kPa

Correct Option: D

Here, P₁ = 100 kPa
T₁ = 27°C
V₄ = V₁ = 10
V₃ V₂

C_v = 0.287 kJ/kgK
P_m × (V₁ – V₂ )= work done
= h₁ – h₂
= 1500 – 700 = 800 kJ
Now P₁V₁ = mRT₁
or 100 × 10³ × V₁ = 1× 0.287 × 10³ × 300
or V₁ = 0.861
∴ V₂ = 0.0861
Now P_m (0.861 – 0.0861) = 800
∴ P_m = 1032 kPa

Which one of the following is NOT a necessary assumption for the air-standard Otto cycle?

1. All processes are internally reversible.
1. Intake and exhaust processes are constant volume heat rejection processes.
1. The combustion process is a constant volume heat addition process.
1. The working fluid is an ideal gas with constant specific heats.

View Hint View Answer Discuss in Forum

Intake process is the constant volume heat addition process
Hence (b) is not the right assumption

Correct Option: B

Intake process is the constant volume heat addition process
Hence (b) is not the right assumption

Direction: In a steam power plant operating on the Rankine cycle, steam enters the turbine at 4 MPa, 350°C and exists at a pressure of 15 kPa. Then it enters the condenser and exists as saturated water. Next, a pump feeds back the water to the boiler. The adiabatic efficiency of the turbine is 90%. The thermodynamic states of water and steam are given in the table.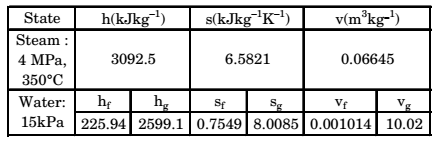

h is specific enthalpy, s is specific entropy and v the specific volume; subscript f and g denote saturated liquid state and saturated vapour state.

Heat supplied (kJ kg^–1) to the cycle is

1. 2372
1. 2576
1. 2863
1. 3092

View Hint View Answer Discuss in Forum

Given: Rankine cycle on T-S diagram
P₃ = 4 MPa
T₃ = 350°C
η_t = 0.9
h₃ =3092.5 kJ/kg
s₃ = s₄ = 6.5821 kJ/kgk
h₁ = 225.94 kJ/kg = h_f
h_g = 2599.1 kJ/kg

h_fg = h_g – h_f = 2373.16 kJ/kg
s₁ = s_f = 0.7549 kJ/kgK
s_g = 8.0085 kJ/kgK
s_fg = 8.0085 – 0.7949 = 7.2536 kJ/kg K
Also, s₃ = s₄ = 6.5821
∴ s₄ = s₁ + x s_fg
= 0.7549 + x (7.2536) = 6.5821
⇒ x = 0.8
h₄ = h₁ + xh_fg
= 225.94 + (0.8 × 2375.16) = 2132.4 kJ/kg
Net work output of the cycle
= η_t (h₃ – h₄)
= 0.9 (3092.5 – 2132.4)
= 864 kJ/kg
≈ 860 kJ/kg
Heat supplied to the cycle = h₃ – h₂
Since we do not have information regarding h₂, therefore neglect compressor work and take
h₂ = h₁
∴ Q_s = 3092.5 – 2866 kJ/kg = 2863 kJ/kg

Correct Option: D

Given: Rankine cycle on T-S diagram
P₃ = 4 MPa
T₃ = 350°C
η_t = 0.9
h₃ =3092.5 kJ/kg
s₃ = s₄ = 6.5821 kJ/kgk
h₁ = 225.94 kJ/kg = h_f
h_g = 2599.1 kJ/kg

h_fg = h_g – h_f = 2373.16 kJ/kg
s₁ = s_f = 0.7549 kJ/kgK
s_g = 8.0085 kJ/kgK
s_fg = 8.0085 – 0.7949 = 7.2536 kJ/kg K
Also, s₃ = s₄ = 6.5821
∴ s₄ = s₁ + x s_fg
= 0.7549 + x (7.2536) = 6.5821
⇒ x = 0.8
h₄ = h₁ + xh_fg
= 225.94 + (0.8 × 2375.16) = 2132.4 kJ/kg
Net work output of the cycle
= η_t (h₃ – h₄)
= 0.9 (3092.5 – 2132.4)
= 864 kJ/kg
≈ 860 kJ/kg
Heat supplied to the cycle = h₃ – h₂
Since we do not have information regarding h₂, therefore neglect compressor work and take
h₂ = h₁
∴ Q_s = 3092.5 – 2866 kJ/kg = 2863 kJ/kg

The net work output (kJ kg^–1) of the cycle is

1. 498
1. 775
1. 860
1. 957

View Hint View Answer Discuss in Forum

Given: Rankine cycle on T-S diagram
P₃ = 4 MPa
T₃ = 350°C
η_t = 0.9
h₃ =3092.5 kJ/kg
s₃ = s₄ = 6.5821 kJ/kgk
h₁ = 225.94 kJ/kg = h_f
h_g = 2599.1 kJ/kg

h_fg = h_g – h_f = 2373.16 kJ/kg
s₁ = s_f = 0.7549 kJ/kgK
s_g = 8.0085 kJ/kgK
s_fg = 8.0085 – 0.7949 = 7.2536 kJ/kg K
Also, s₃ = s₄ = 6.5821
∴ s₄ = s₁ + x s_fg
= 0.7549 + x (7.2536) = 6.5821
⇒ x = 0.8
h₄ = h₁ + xh_fg
= 225.94 + (0.8 × 2375.16) = 2132.4 kJ/kg
Net work output of the cycle
= η_t (h₃ – h₄)
= 0.9 (3092.5 – 2132.4)
= 864 kJ/kg
≈ 860 kJ/kg
Heat supplied to the cycle = h₃ – h₂
Since we do not have information regarding h₂, therefore neglect compressor work and take
h₂ = h₁
∴ Q_s = 3092.5 – 2866 kJ/kg = 2863 kJ/kg

Correct Option: A

Given: Rankine cycle on T-S diagram
P₃ = 4 MPa
T₃ = 350°C
η_t = 0.9
h₃ =3092.5 kJ/kg
s₃ = s₄ = 6.5821 kJ/kgk
h₁ = 225.94 kJ/kg = h_f
h_g = 2599.1 kJ/kg

h_fg = h_g – h_f = 2373.16 kJ/kg
s₁ = s_f = 0.7549 kJ/kgK
s_g = 8.0085 kJ/kgK
s_fg = 8.0085 – 0.7949 = 7.2536 kJ/kg K
Also, s₃ = s₄ = 6.5821
∴ s₄ = s₁ + x s_fg
= 0.7549 + x (7.2536) = 6.5821
⇒ x = 0.8
h₄ = h₁ + xh_fg
= 225.94 + (0.8 × 2375.16) = 2132.4 kJ/kg
Net work output of the cycle
= η_t (h₃ – h₄)
= 0.9 (3092.5 – 2132.4)
= 864 kJ/kg
≈ 860 kJ/kg
Heat supplied to the cycle = h₃ – h₂
Since we do not have information regarding h₂, therefore neglect compressor work and take
h₂ = h₁
∴ Q_s = 3092.5 – 2866 kJ/kg = 2863 kJ/kg

A thermal power plant operates on a regenerative cycle with a single open feedwater heater, as shown in the figure. For the state points shown, the specific enthalpies are: h₁ = 2800 kJ/kg and h₂ = 200 kJ/kg. The bleed to the feedwater heater is 20% of the boiler steam generation rate. The specific enthalpy at state 3 is

1. 720 kJ/kg
1. 2280 kJ/kg
1. 1500 kJ/kg
1. 3000 kJ/kg

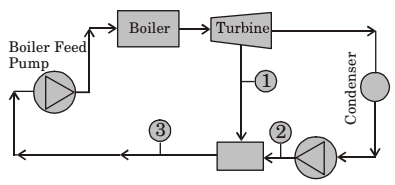
View Hint View Answer Discuss in Forum

h₃ = 0.2h₁ + h₂ × 0.8
= 560 + 160 = 720 kJ/kg

Correct Option: A

h₃ = 0.2h₁ + h₂ × 0.8
= 560 + 160 = 720 kJ/kg

	V₄	=	V₁	= 10
	V₃		V₂

	V₄	=	V₁	= 10
	V₃		V₂

Thermodynamics Miscellaneous

Thermodynamics Miscellaneous

Thermodynamics

Correct Option: D

Correct Option: B

Correct Option: D

Correct Option: A

Correct Option: A