Ratio, Proportion
- The ratio of the incomes of A and B as well as of B and C is 3 : 2. If one third of A’s income exceeds one fourth of C's income by ₹ 1000, what is B’s income in ?
-
View Hint View Answer Discuss in Forum
A : B = 3 : 2 = 9 : 6
B : C = 3 : 2 = 6 : 4
∴ A : B : C = 9 : 6 : 4∴ 9x − 4x = 1000 3 4
⇒ 3x – x = 1000
⇒ 2x = 1000
⇒ x = 500
∴ B’s income = 6x = 6 × 500
= ₹ 3000Correct Option: A
A : B = 3 : 2 = 9 : 6
B : C = 3 : 2 = 6 : 4
∴ A : B : C = 9 : 6 : 4∴ 9x − 4x = 1000 3 4
⇒ 3x – x = 1000
⇒ 2x = 1000
⇒ x = 500
∴ B’s income = 6x = 6 × 500
= ₹ 3000
- The income of A and B are in the ratio 2 : 3 and their expenditures are in the ratio 1 : 2. If each saves ₹ 24,000, find A’s income.
-
View Hint View Answer Discuss in Forum
Let the income of A and B be ₹ 2x and ₹ 3x. and their expenditures be ₹ y and ₹ 2y respectively.
∴ 2x – y = 24000 ...(i)
and 3x – 2y = 24000 ...(ii)
By equation (i) × 2 – (ii),
4x – 2y – 3x + 2y = 24000
⇒ x = 24000
∴ A’s income = 2 × 24000
= ₹ 48000Correct Option: D
Let the income of A and B be ₹ 2x and ₹ 3x. and their expenditures be ₹ y and ₹ 2y respectively.
∴ 2x – y = 24000 ...(i)
and 3x – 2y = 24000 ...(ii)
By equation (i) × 2 – (ii),
4x – 2y – 3x + 2y = 24000
⇒ x = 24000
∴ A’s income = 2 × 24000
= ₹ 48000
- The incomes of A and B are in the ratio 3 : 2 and their expenditures are in the ratio 5 : 3. If each saves Rs. 1000, then A’s income is
-
View Hint View Answer Discuss in Forum
Let incomes of A and B be Rs. 3x and Rs. 2x respectively. Let the expenditures of A and B be Rs. 5y and Rs. 3y respectively.
According to the question,
3x – 5y = Rs. 1000 .... (i)
2x – 3y = Rs. 1000 .... (ii)
By equation (i) × 2 – (ii) × 3,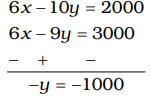
∴ y = 1000
From equation (i),
3x – 5 × 1000 = 1000
⇒ 3x = 1000 + 5000 = Rs. 6000
= A’s incomeCorrect Option: A
Let incomes of A and B be Rs. 3x and Rs. 2x respectively. Let the expenditures of A and B be Rs. 5y and Rs. 3y respectively.
According to the question,
3x – 5y = Rs. 1000 .... (i)
2x – 3y = Rs. 1000 .... (ii)
By equation (i) × 2 – (ii) × 3,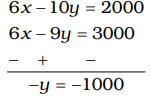
∴ y = 1000
From equation (i),
3x – 5 × 1000 = 1000
⇒ 3x = 1000 + 5000 = Rs. 6000
= A’s income
- A bag contains ₹ 90 in coins of denominations of 50 paise, 25 paise and 10 paise. If coins of 50 paise, 25 paise and 10 paise are in the ratio 2 : 3 : 5, then the number of 25 paise coins in the bag is
-
View Hint View Answer Discuss in Forum
Ratio of values of 50 paise, 25 paise and 10 paise coins
= 2 : 3 : 5 2 4 10 = 1 : 3 : 1 4 2
= 4 : 3 : 2
Sum of the ratios = 4 + 3 + 2 = 9Value of 25 paise coins = 3 × 90 = ₹ 30 9
Number of 25 paise coins
= 30 × 4 = 120Correct Option: B
Ratio of values of 50 paise, 25 paise and 10 paise coins
= 2 : 3 : 5 2 4 10 = 1 : 3 : 1 4 2
= 4 : 3 : 2
Sum of the ratios = 4 + 3 + 2 = 9Value of 25 paise coins = 3 × 90 = ₹ 30 9
Number of 25 paise coins
= 30 × 4 = 120
- If 378 coins consist of rupees, 50 paise and 25 paise coins, whose values are in the ratio of 13 : 11 : 7, the number of 50 paise coins will be :
-
View Hint View Answer Discuss in Forum
The ratio of values of rupee,
50 paise and 25 paise coins = 13 : 11 : 7
∴ Ratio of their numbers
= 13 × 1 : 11 × 2 : 7 × 4
= 13 : 22 : 28
Sum of the ratios
= 13 + 22 + 28 = 63
∴ Required number of 50 paise coins= 22 × 378 = 132 63 Correct Option: A
The ratio of values of rupee,
50 paise and 25 paise coins = 13 : 11 : 7
∴ Ratio of their numbers
= 13 × 1 : 11 × 2 : 7 × 4
= 13 : 22 : 28
Sum of the ratios
= 13 + 22 + 28 = 63
∴ Required number of 50 paise coins= 22 × 378 = 132 63

