Engineering Mathematics Miscellaneous Easy Questions and Answers | Page - 31

Engineering Mathematics Miscellaneous

The partial differential equation

1. degree 1, order 2
1. degree, 1 order 1
1. degree 2, order 1
1. degree 2, order 2

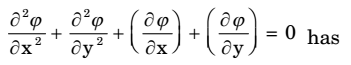
View Hint View Answer Discuss in Forum

A order is 2 and degree is 1.

Correct Option: A

A order is 2 and degree is 1.

A differential equation is given as
x² d²y - 2x dy + 2y = 4
dx² dx

The solution of the differential equation in terms of arbitrary constants C₁ and C₂ is

1. y = C₁ x² + C₂ x + 4
1. y = C₁ + C₂x + 2
  x²
1. y = C₁ x² + C₂ x + 2
1. y = C₁ + C₂x + 4
  x²

View Hint View Answer Discuss in Forum

x² = d²y - 2x dy + 2y = 4
dx² d

Let x = e^z
CF : d²y = θ(θ - 1)
dx²

⇒ θ(θ - 1) - 2θ + 2 = 0
⇒ θ² - 3θ + 2 = 0
(θ - 1)(θ - 2) = 0
θ = 1,2
θ = C₁e^z + C₁e^2z
y = C₁x² + C₂x
PI : - 4 + 4
(θ - 1) (θ - 2)

= + 4(1 -θ)^-1 - 4 1 - θ ^-1
2 2

= + 4(1 - θ + ...) - 2 1 + θ + .....
2

= + 4 – 2 = 2 (Neglecting higher order term)
y = CF + PI
y = C₁ x² C₂ x + 2

Correct Option: C

x² = d²y - 2x dy + 2y = 4
dx² d

Let x = e^z
CF : d²y = θ(θ - 1)
dx²

⇒ θ(θ - 1) - 2θ + 2 = 0
⇒ θ² - 3θ + 2 = 0
(θ - 1)(θ - 2) = 0
θ = 1,2
θ = C₁e^z + C₁e^2z
y = C₁x² + C₂x
PI : - 4 + 4
(θ - 1) (θ - 2)

= + 4(1 -θ)^-1 - 4 1 - θ ^-1
2 2

= + 4(1 - θ + ...) - 2 1 + θ + .....
2

= + 4 – 2 = 2 (Neglecting higher order term)
y = CF + PI
y = C₁ x² C₂ x + 2

Given the ordinary differential equation
d²y + dy = 0
dx² dx

with(0) = 0 and dy (0) = 1, the value of y(1) is
dx

_______ (correct to two decimal places).

1. 1.4678
1. 1.4628
1. 1.4698
1. 1.46

View Hint View Answer Discuss in Forum

(D² + D – 6) y = 0
y (0) = 0,
y' (0) = 1
(D + 3) (D – 2) y = 0
D = 2, – 3
C .F. = C₁ e^2x + C₂ e^–3x
y = c₁ e^2x + C₂ e^–3x
y (0) = 0
So, 0 = C₁ + C₂ ----------------------(i)
y = (1) = e² - e^{- 3} = 1.4678
5

y (0) = 1
1 = 2 C₁ – 3 C₂ ___(ii)
From equations (i) & (ii), we get
C₁ = 1 , C₂ = - 1
5 5

y = e^2x - e^{- 3x}
5 5

when, x = 1
y = (1) = e² - e^{- 3} = 1.4678
5

Correct Option: A

(D² + D – 6) y = 0
y (0) = 0,
y' (0) = 1
(D + 3) (D – 2) y = 0
D = 2, – 3
C .F. = C₁ e^2x + C₂ e^–3x
y = c₁ e^2x + C₂ e^–3x
y (0) = 0
So, 0 = C₁ + C₂ ----------------------(i)
y = (1) = e² - e^{- 3} = 1.4678
5

y (0) = 1
1 = 2 C₁ – 3 C₂ ___(ii)
From equations (i) & (ii), we get
C₁ = 1 , C₂ = - 1
5 5

y = e^2x - e^{- 3x}
5 5

when, x = 1
y = (1) = e² - e^{- 3} = 1.4678
5

Consider the differential equation 3y"(x) + 27y(x) = 0 with initial conditions y(0) and y'(0) = 2000. The value of y at x = 1 is _________.

1. 94.08
1. 95
1. 94.58
1. 94

View Hint View Answer Discuss in Forum

The D.E. is 3y (x) + 27 y (x) = 0
The auxiliary equation is
3 m² + 27 = 0 m² + 9 = 0
m = ≠ 3i Solution is y = C₁ cos 3x + C₂ sin 3x
Given that y (0) = 0
∴ 0 = C₁
y' = –3 C₁. sin 3x + 3 c₂ cos 3x
y' (0) = 2000
2000 = 0 + 3 C₂
C₂ = 2000
3

∴ Solution is
y = 2000 sin 3x
3

when x = 1, y = 2000 sin 3 = 94.08
3

Correct Option: A

The D.E. is 3y (x) + 27 y (x) = 0
The auxiliary equation is
3 m² + 27 = 0 m² + 9 = 0
m = ≠ 3i Solution is y = C₁ cos 3x + C₂ sin 3x
Given that y (0) = 0
∴ 0 = C₁
y' = –3 C₁. sin 3x + 3 c₂ cos 3x
y' (0) = 2000
2000 = 0 + 3 C₂
C₂ = 2000
3

∴ Solution is
y = 2000 sin 3x
3

when x = 1, y = 2000 sin 3 = 94.08
3

For a position vector r = xî + yĵ + zk̂ the norm of the vector can be defined as
| r | = √x² + y² + z² . Given a function Φ = In | r |, its gradient ∇Φ is

1. r
1. r
  | r |
1. r
  r.r
1. r
  | r |³

View Hint View Answer Discuss in Forum

r
r.r

Correct Option: C

r
r.r