Engineering Mathematics Miscellaneous

Engineering Mathematics Miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Engineering Mathematics

Engineering Mathematics Miscellaneous
  1. Let X1, X2 be two independent normal random variables with means μ1, μ2 and standard deviations σ1, σ2 respectively. Consider Y = X1 – X2; μ1 = μ2 = 1, σ1 = 1, σ2 = 2, Then,








  1. View Hint View Answer Discuss in Forum


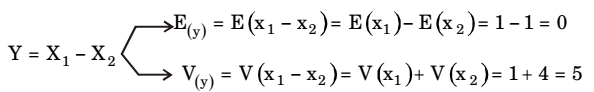
    Y is normally distributed wit h mean 0 and variance 5.

    Correct Option: B


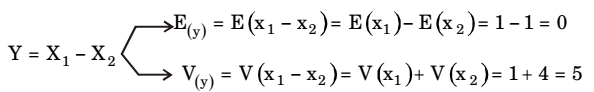
    Y is normally distributed wit h mean 0 and variance 5.

  1. Consider a Poisson distribution for the tossing of a biased coin. The mean for this distribution is μ. The standard deviation for this distribution is given by








  1. View Hint View Answer Discuss in Forum

    Standard deviation √Variance = √μ

    Correct Option: A

    Standard deviation √Variance = √μ

  1. A machine produces 0, 1 or 2 defective pieces in a day with associated probability of 1/6, 2/3 and 1/6, respectively. The mean value and the variance of the number of defective pieces produced by the machine in a day, respectively, are








  1. View Hint View Answer Discuss in Forum

    Let ‘x’ be no. of defective pieces.

    Mean (μ) = E(x) = ∑ x P(x)

    =0 ×
    1
    		+1 ×
    1
    		+2 ×
    1
    636

    = 0 +
    2
    		+
    1
    		= 1
    33

    E(x2) = ∑ x2 P(x)
    =0 ×
    1
    		+1 ×
    2
    		+4 ×
    1
    636

    = 0 +
    2
    		+
    2
    		=
    4
    333

    Variance, V(x) = E(x2) – {E(x)}2
    =
    4
    		- 1 =
    1
    33

    Correct Option: A

    Let ‘x’ be no. of defective pieces.

    Mean (μ) = E(x) = ∑ x P(x)

    =0 ×
    1
    		+1 ×
    1
    		+2 ×
    1
    636

    = 0 +
    2
    		+
    1
    		= 1
    33

    E(x2) = ∑ x2 P(x)
    =0 ×
    1
    		+1 ×
    2
    		+4 ×
    1
    636

    = 0 +
    2
    		+
    2
    		=
    4
    333

    Variance, V(x) = E(x2) – {E(x)}2
    =
    4
    		- 1 =
    1
    33

  1. In the following table, x is a discrete random variable and p(x) is the probability density. The standard deviation of x is








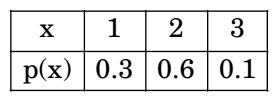
  1. View Hint View Answer Discuss in Forum

    Given

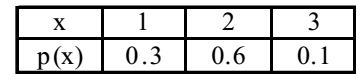
    mean (μ) = exp(x) = 1 × 0.3 + 2 × 0.6 + 3 × 0.1
    = 0.3 + 1.2 + 0.3 = 1.8
    E(x2) = ∑ x2P(x)
    = 1 × 0.3 + 4 × 0.6 + 9 × 0.1
    = 0.3 + 2.4 + 0.9 = 3.6
    Variance v (x) = E (x2) – μ2 = 3.6 – (1.8)2
    S.D(σ) = + √υ(x)
    = + √3.6 - (1.8)2
    = √0.36 = 0.6

    Correct Option: D

    Given

    mean (μ) = exp(x) = 1 × 0.3 + 2 × 0.6 + 3 × 0.1
    = 0.3 + 1.2 + 0.3 = 1.8
    E(x2) = ∑ x2P(x)
    = 1 × 0.3 + 4 × 0.6 + 9 × 0.1
    = 0.3 + 2.4 + 0.9 = 3.6
    Variance v (x) = E (x2) – μ2 = 3.6 – (1.8)2
    S.D(σ) = + √υ(x)
    = + √3.6 - (1.8)2
    = √0.36 = 0.6

  1. The standard deviation of a uniformly distributed random variable between 0 and 1 is








  1. View Hint View Answer Discuss in Forum

    Variance,

    V(x) =
    (b - a)2
    		=
    (1 - 0)2
    1212

    ∴ Standard deviation,
    σ =
    1
    √12

    Correct Option: A

    Variance,

    V(x) =
    (b - a)2
    		=
    (1 - 0)2
    1212

    ∴ Standard deviation,
    σ =
    1
    √12