Engineering Mathematics Miscellaneous
-
A calculator has accuracy up to 8 digits after decimal place. The value of 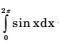
when evaluated using this calculator by trapezoidal method with 8 equal intervals, to 5 significant digits is
-
View Hint View Answer Discuss in Forum
h = 2π - 0 = π 8 4
y0 = sin (0) = 0y1 = sin 
π 
= 0.7071 4 y2 = sin 
π 
= 1 2 y3 = sin 
3π 
= 0.7071 4
y4 = sin (π) = 0y5 = sin 
5π 
= -0.7071 4 y6 = sin 
6π 
= -1 4 y7 = sin 
7π 
= -0.7071 4 y8 = sin 
8π 
= 0 4
Trapezoidal rule
h [ y0 + yn + 2(y1 + y2 + ... + yn - 1) ] 2 
[(0 + 0) + 2 (0.7071 + 1 + .7071 + -0.7071 - 0.7071)] = 0Correct Option: A
h = 2π - 0 = π 8 4
y0 = sin (0) = 0y1 = sin 
π 
= 0.7071 4 y2 = sin 
π 
= 1 2 y3 = sin 
3π 
= 0.7071 4
y4 = sin (π) = 0y5 = sin 
5π 
= -0.7071 4 y6 = sin 
6π 
= -1 4 y7 = sin 
7π 
= -0.7071 4 y8 = sin 
8π 
= 0 4
Trapezoidal rule
h [ y0 + yn + 2(y1 + y2 + ... + yn - 1) ] 2 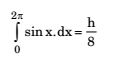
[(0 + 0) + 2 (0.7071 + 1 + .7071 + -0.7071 - 0.7071)] = 0
- An analytic function of a complex variable z = x + iy is expressed as f(z) = u(x, y)+ iv(x, y), where i = √-1. If u(x, y) = x2 - y2, then expression for v(x, y) in terms of x, y and a general constant c would be
-
View Hint View Answer Discuss in Forum
Given f(z) = μx(x, y) + iv (x, y) is analytic and x = x2 - y2
We know that if f(z) = μ + iv is analytic then C-R equations will be satisfied.i.e. ∂μ = ∂v and ∂μ = - ∂v ∂x ∂y ∂y ∂x
∴ v = 2xy + c is correct answer
Correct Option: C
Given f(z) = μx(x, y) + iv (x, y) is analytic and x = x2 - y2
We know that if f(z) = μ + iv is analytic then C-R equations will be satisfied.i.e. ∂μ = ∂v and ∂μ = - ∂v ∂x ∂y ∂y ∂x
∴ v = 2xy + c is correct answer
- An analytic function of a complex variable z = x + iy is expressed as f(z) = u(x, y)+ iv(x, y), where i = √-1. If u(x, y) = 2xy, then v(x, y) must be
-
View Hint View Answer Discuss in Forum
Given f(z) = u + iv is analytic and u = 2xy
We know that if f(z) is analytic then CR equations will be satisfied.i.e. ∂u = ∂v and ∂u = - ∂v ∂x ∂y ∂y ∂x
Verify the options which satisfy the above C-R equations.
v = – x2 + y2 + constant, satisfies the C-R equation.Correct Option: C
Given f(z) = u + iv is analytic and u = 2xy
We know that if f(z) is analytic then CR equations will be satisfied.i.e. ∂u = ∂v and ∂u = - ∂v ∂x ∂y ∂y ∂x
Verify the options which satisfy the above C-R equations.
v = – x2 + y2 + constant, satisfies the C-R equation.
- If(z) = u(x, y) + iv(x, y) is an analytic function or complex variable z = x + iy where i = √-1 , u (x, y) = 2 xy, then v(x, y) may be expressed as
-
View Hint View Answer Discuss in Forum
Given f(z) = u + iv is analytic and u = 2xy We know that if f(z) is analytic then CR equations will be satisfied.
i.e. ∂u = ∂v ∂x ∂y and ∂u = - ∂v ∂y ∂x
Verify the options which satisfy the above C-R equations.
v = – x2 + y2 + constant, satisfies the C-R equation.Correct Option: A
Given f(z) = u + iv is analytic and u = 2xy We know that if f(z) is analytic then CR equations will be satisfied.
i.e. ∂u = ∂v ∂x ∂y and ∂u = - ∂v ∂y ∂x
Verify the options which satisfy the above C-R equations.
v = – x2 + y2 + constant, satisfies the C-R equation.
- An analytic function of a complex variable z = x + iy is expressed as f(z) = u(x, y) + i v(x, y) where i = √-1. If u = xy, the expression for v should be
-
View Hint View Answer Discuss in Forum
Given u = x,y
For analytic function∂u = ∂v ∂x ∂y and ∂u = - ∂v ∂y ∂x
By Milne Thomson method
Let w = u + zv∴ dw = ∂y + i ∂v dz ∂x ∂x = ∂u - i ∂u ∂x ∂y or dw = y - ix dz
Replacing x by z and y by 0, we getdw = 0 - iz dz
where , z = x + iy
∴ dw = - iz dzIntegrating , w = -i z2 + C 2
where C is a constant ,∴ V = Im 
-i z2 + C 
2 = Im 
-i (x2 - y2 + 2ixy) + C 
2 or V = y2 - x2 2
Correct Option: C
Given u = x,y
For analytic function∂u = ∂v ∂x ∂y and ∂u = - ∂v ∂y ∂x
By Milne Thomson method
Let w = u + zv∴ dw = ∂y + i ∂v dz ∂x ∂x = ∂u - i ∂u ∂x ∂y or dw = y - ix dz
Replacing x by z and y by 0, we getdw = 0 - iz dz
where , z = x + iy
∴ dw = - iz dzIntegrating , w = -i z2 + C 2
where C is a constant ,∴ V = Im 
-i z2 + C 
2 = Im 
-i (x2 - y2 + 2ixy) + C 
2 or V = y2 - x2 2

