Engineering Mathematics Miscellaneous
- Consider the shaded triangular region P shown in the figure. What is ∬P xy dxdy ?

-
View Hint View Answer Discuss in Forum
I = ∬ xy .dxdy
The limit of y is from 0 to 
and limit of x from 0 to 2. 

= 
x 
1 - x 
2 dx 2 2 = 1 
x(x² + 4 - 4x).dx 8 = 1 
(x³ + 4x - 4x²).dx 8 
Correct Option: A
I = ∬ xy .dxdy
The limit of y is from 0 to 
and limit of x from 0 to 2. 

= 
x 
1 - x 
2 dx 2 2 = 1 
x(x² + 4 - 4x).dx 8 = 1 
(x³ + 4x - 4x²).dx 8 
- The right circular cone of largest volume that can be enclosed by a sphere of 1 m radius has a height of
-
View Hint View Answer Discuss in Forum

Given R = 1, radins of sphere.
Let height of cone is H = h + RVolume , V = 1 π × (√R² - h²)2(R + h) 3
for maximum value ,⇒ dV = 0 dh ⇒ d 
1 (R² - h²)(R + h) 
dh 3
⇒ -2h(R + h) + (R² - h²) = 0
⇒ (R + h)(R - 3h) = 0h = -R , R 3 Height of the come = R + R = 4R 3 3 = 4 × 1 m = 4 m 3 3
Correct Option: D

Given R = 1, radins of sphere.
Let height of cone is H = h + RVolume , V = 1 π × (√R² - h²)2(R + h) 3
for maximum value ,⇒ dV = 0 dh ⇒ d 
1 (R² - h²)(R + h) 
dh 3
⇒ -2h(R + h) + (R² - h²) = 0
⇒ (R + h)(R - 3h) = 0h = -R , R 3 Height of the come = R + R = 4R 3 3 = 4 × 1 m = 4 m 3 3
-
The length of the curve y = 2 x3 / 2 between x = 0 and x = 1 is 3
-
View Hint View Answer Discuss in Forum
The length is given by ∫√(dy)² + (dx)²
∫√x(dy)² + (dx)²
dx = √x .dy∴ L = 
(√x + 1) . dx 
= 1.22
Correct Option: D
The length is given by ∫√(dy)² + (dx)²
∫√x(dy)² + (dx)²
dx = √x .dy∴ L = 
(√x + 1) . dx 
= 1.22
- Changing the order of the integration in the double integral

leads to 
.What is q ?
-
View Hint View Answer Discuss in Forum
When I = 
f(x , y) dydx 
I = 
f(x , y) dxdy Correct Option: A
When I = 
f(x , y) dydx 
I = 
f(x , y) dxdy
-
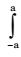
(sin6x + sin7x) dx is equal to
-
View Hint View Answer Discuss in Forum
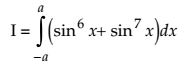
= 2 
sin6x dx + 0 = 2 
sin6x dx = 2 
sin6x dx + 0
Correct Option: A
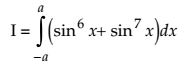
= 2 
sin6x dx + 0 = 2 
sin6x dx = 2 
sin6x dx + 0

