156. The divergence of the vector field
     u = e^x (cos yî + sin yĵ) is

1. 1. 0

   
   
   

   2. e^x cosy + e^x sin y

   
   
   

   3. 2 e^x cos y

   
   
   

   4. 2 e^x sin y

   
   
   

---

1. View Hint View Answer Discuss in Forum

   u = e^xcos yî + e^xsinyĵ
   

   ∇ . u =	δ	(u1) +	δ	(u2)
   	δx		δy

   
   

   =	δ	(ex . cos y) +	δ	(ex . sin y)
   	δx		δy

   
   = e^xcosy + e^xcosy = 2e^xcosy

   Correct Option: C

   u = e^xcos yî + e^xsinyĵ
   

   ∇ . u =	δ	(u1) +	δ	(u2)
   	δx		δy

   
   

   =	δ	(ex . cos y) +	δ	(ex . sin y)
   	δx		δy

   
   = e^xcosy + e^xcosy = 2e^xcosy

---

157. The divergence of the vector –yi + xj is _____

1. 1. 0

   
   
   

   2. 1

   
   
   

   3. 2

   
   
   

   4. 3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   F = -yî + xĵ
   

   ∇ . F =	δ	(-y) +	δ	(x)
   	δx		δy

   
   = 0 + 0 = 0

   Correct Option: A

   F = -yî + xĵ
   

   ∇ . F =	δ	(-y) +	δ	(x)
   	δx		δy

   
   = 0 + 0 = 0

---

---

158. For the vector V = 2yzî + 3xzĵ + 4xyk̂ of ∇(∇ × V) is _________.

1. 1. -0

   
   
   

   2. -1

   
   
   

   3. 1

   
   
   

   4. 0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given vector V = 2yzî + 3xzĵ - xyk̂
   
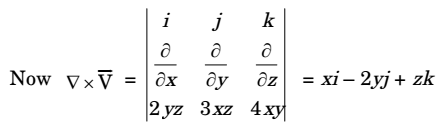
   ∇ . (∇ × V) = 1 - 2 + 1 =0

   Correct Option: D

   Given vector V = 2yzî + 3xzĵ - xyk̂
   
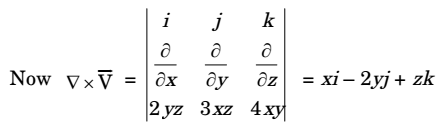
   ∇ . (∇ × V) = 1 - 2 + 1 =0

---

159. The value of the line integral ∮F . rds , where C is a circle of radius units is ________
     Here, F ( x, y ) = yî + 2xĵ and r̂ is the UNIT tangent vector on the curve C at an arc length s from a reference point on the curve î and î are the basis vectors in the x – y Cartesian reference. In evaluating the line integral, the curve has to be traversed in the counterclockwise direction.

1. 1. 18

   
   
   

   2. 13

   
   
   

   3. 16

   
   
   

   4. 15

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ∫_c F . r ds = ∫_c F . dr = ∫_c F₁dx + F₂dy
   

   ∬R		δF2		- δF1			dxdy
   		δ		δ

   
   F₁ = y, F₂ = 2x
   ∬_R (2 - 1)dxdy
   

   Correct Option: C

   ∫_c F . r ds = ∫_c F . dr = ∫_c F₁dx + F₂dy
   

   ∬R		δF2		- δF1			dxdy
   		δ		δ

   
   F₁ = y, F₂ = 2x
   ∬_R (2 - 1)dxdy
   

---

---

160. A scalar potential φ has the following gradient:
     vφ = yZî + xZĵ + xyk̂ . Consider the integral
     ∫_c φ.dr on the curve r = xî + yĵ + ẑ
     The curve C is parameterized as follows:
     

     		x = t	and 1 ≤ t ≤ 3
     		y = t
     		z = 3t2

     
     The value of the integral is ________

1. 1. 721

   
   
   

   2. 722

   
   
   

   3. 716

   
   
   

   4. 726

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ∫_c ∇Φ . dr = ∫_c(yzî + xzĵ + xyk̂)(dxî + dyĵ + dzk̂
   = ∫_c (yzdx + xzdy + xydz) = xyz
   Given that x = t, y = t², z = 3t²
   = t.t² . 3t²|₁³
   = 3(t⁵) |₁²
   = 3(3⁵ - 1)
   = 726

   Correct Option: D

   ∫_c ∇Φ . dr = ∫_c(yzî + xzĵ + xyk̂)(dxî + dyĵ + dzk̂
   = ∫_c (yzdx + xzdy + xydz) = xyz
   Given that x = t, y = t², z = 3t²
   = t.t² . 3t²|₁³
   = 3(t⁵) |₁²
   = 3(3⁵ - 1)
   = 726

---