Engineering Mathematics Miscellaneous

Engineering Mathematics Miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Engineering Mathematics

Engineering Mathematics Miscellaneous
  1. Which one of the following describes the relationship among the three vectors, î + ĵ + k̂, 2î + 3ĵ + k̂ and 5î + 6ĵ + 4k̂?








  1. View Hint View Answer Discuss in Forum

    Given vectors are
    i + j + k, 2i + 3j + k and 5i + 6j + k

    1
    1
    1
    		= 0
    231
    561

    ∴ Vectors are linearly dependent.

    Correct Option: B

    Given vectors are
    i + j + k, 2i + 3j + k and 5i + 6j + k

    1
    1
    1
    		= 0
    231
    561

    ∴ Vectors are linearly dependent.

  1. The following surface integral is to be evaluated over a sphere for the given steady velocity vector field F = xî + yĵ + zk̂ defined with respect to a Cartesian coordinate system having i, j and k as unit base vectors.
    ∬s ( F.n )dA
    where S is the sphere, x2 + y2 + z3 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral is








  1. View Hint View Answer Discuss in Forum

    Use Gauss-Divergence theorem,

    I = ∬s
    1
    		F.n̂dA
    4

    = ∭v ∇.FdV
    ∇.F = 1 + 1 + 1 = 3
    ∴ I =
    1
    		× 3V =
    3
    		×
    4
    		π(1)3 = π
    443

    Correct Option: A

    Use Gauss-Divergence theorem,

    I = ∬s
    1
    		F.n̂dA
    4

    = ∭v ∇.FdV
    ∇.F = 1 + 1 + 1 = 3
    ∴ I =
    1
    		× 3V =
    3
    		×
    4
    		π(1)3 = π
    443

  1. For the spherical surface x2 + y2 + z2 = 1, the unit outward normal vector at the point
    1
    		,
    1
    		, 0is given by
    √2√2








  1. View Hint View Answer Discuss in Forum

    Given spherical surface is x2 + y2 + z2 = 1
    and point is

    1
    		,
    1
    		, 0
    √2√2

    Normal vector outward to x2 + y2 + z2 – 1 = 0 at
    1
    		,
    1
    		, 0is
    √2√2

    1
    		i +
    1
    		j + 0.k
    √2√2

    =
    1
    		i +
    1
    		j
    √2√2

    Hence outward unit normal vector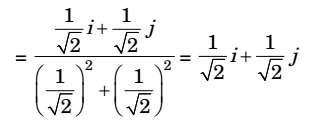

    Correct Option: A

    Given spherical surface is x2 + y2 + z2 = 1
    and point is

    1
    		,
    1
    		, 0
    √2√2

    Normal vector outward to x2 + y2 + z2 – 1 = 0 at
    1
    		,
    1
    		, 0is
    √2√2

    1
    		i +
    1
    		j + 0.k
    √2√2

    =
    1
    		i +
    1
    		j
    √2√2

    Hence outward unit normal vector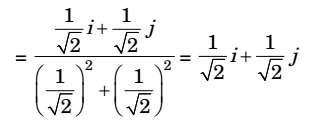

  1. The divergence of the vector field 3xzî + 2xyĵ - yz2k̂ at a point (1, 1, 1) is equal to








  1. View Hint View Answer Discuss in Forum

    F = 3xzi + 2xyj - yz2k

    ∴ div = ∇ . F =
    δ
    		(3xz) +
    δ
    		-
    δ
    		(yz2)
    δxδyδz

    = 3z + 2x –2yz
    At point (1, 1, 1),
    divergence = 3 + 2 –2 = 3

    Correct Option: C

    F = 3xzi + 2xyj - yz2k

    ∴ div = ∇ . F =
    δ
    		(3xz) +
    δ
    		-
    δ
    		(yz2)
    δxδyδz

    = 3z + 2x –2yz
    At point (1, 1, 1),
    divergence = 3 + 2 –2 = 3

  1. The directional derivative of the scalar function f(x, y, z) = x2 + 2y2 + z at the point P = (1, 1, 2) in the direction of the vector a = 3î - 4ĵ is








  1. View Hint View Answer Discuss in Forum

    The directional derivative of a function Φ along a vector A is given by,

    (grad Φ).
    A
    | A |

    Hence directional derivative is
    (grad (x2 + 2y2 + z)).
    (3î - 4ĵ)
    √32 + 42

    (2xî + 4yĵ + k̂),
    (3î - 4ĵ)
    5

    =
    6x - 16y
    5

    Hence (1, 1, 2), directional derivative
    =
    6 × 1 - 16 × 1
    		= - 2
    5

    Correct Option: B

    The directional derivative of a function Φ along a vector A is given by,

    (grad Φ).
    A
    | A |

    Hence directional derivative is
    (grad (x2 + 2y2 + z)).
    (3î - 4ĵ)
    √32 + 42

    (2xî + 4yĵ + k̂),
    (3î - 4ĵ)
    5

    =
    6x - 16y
    5

    Hence (1, 1, 2), directional derivative
    =
    6 × 1 - 16 × 1
    		= - 2
    5