Engineering Mathematics Miscellaneous
- If φ(x, y) and ψ (x, y) are functions with continuous second derivatives, then φ(x, y) + iψ(x, y)
-
View Hint View Answer Discuss in Forum
Can be expressed as an analytic function of
φ + iψ(i = √-1) , when The necessary condition for a function
f (z) = φ(x,y) + i ψ (x, y) to be analytic(i) δφ = δψ δx δy (ii) δφ = -δψ δy δx
are known as Cauchy Rieman equations, providedδφ , δφ , δψ , δψ exists. δx δy δx δy
Correct Option: B
Can be expressed as an analytic function of
φ + iψ(i = √-1) , when The necessary condition for a function
f (z) = φ(x,y) + i ψ (x, y) to be analytic(i) δφ = δψ δx δy (ii) δφ = -δψ δy δx
are known as Cauchy Rieman equations, providedδφ , δφ , δψ , δψ exists. δx δy δx δy
- The function f(t) satisfies the differential equation (d²f / dt²) + f = 0 and the auxilliary conditions, f(0) = 0, (df / dt) (o) = 4. The Laplace transform of f(t) is given by
-
View Hint View Answer Discuss in Forum
Check by options
L-1 
4 
= 4 sint satisfies d²f + f = 0 s² + 1 dt²
Correct Option: C
Check by options
L-1 
4 
= 4 sint satisfies d²f + f = 0 s² + 1 dt²
- If F(s) is the Laplace transform of function f(t), then Laplace transform of

-
View Hint View Answer Discuss in Forum

Correct Option: B

-
View Hint View Answer Discuss in Forum
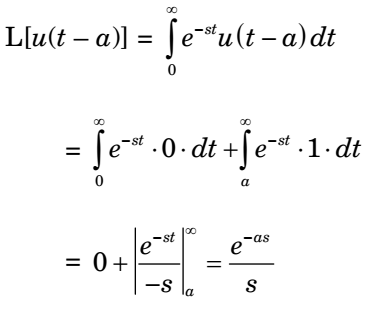
Correct Option: B
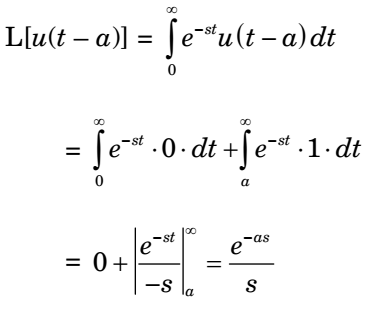
- Laplace transform of the function sin ωt is
-
View Hint View Answer Discuss in Forum
Laplace transforms,
L[sin(ωt)] ω S² + ω² L[cos(ωt)] ω S² + ω²
Correct Option: B
Laplace transforms,
L[sin(ωt)] ω S² + ω² L[cos(ωt)] ω S² + ω²


