Engineering Mathematics Miscellaneous
- Starting from x0 = 1, one step of NewtonRaphson method in solving the equation x3 + 3x – 7 = 0 gives the next value (x1) as
-
View Hint View Answer Discuss in Forum
By N-R method, xn+1 = xn - f(x) , x0 = 1 f'(x)
f(x) = x3 + 3x - 7
⇒ f(1) = -3,⇒ x1 = x0 - f(x0) f'(x0)
⇒ f(x) = 3x² + 3,
⇒ f(1) = 6,x4 = 1 - -3 = 1 - (-0.5) =1.5 6
Correct Option: C
By N-R method, xn+1 = xn - f(x) , x0 = 1 f'(x)
f(x) = x3 + 3x - 7
⇒ f(1) = -3,⇒ x1 = x0 - f(x0) f'(x0)
⇒ f(x) = 3x² + 3,
⇒ f(1) = 6,x4 = 1 - -3 = 1 - (-0.5) =1.5 6
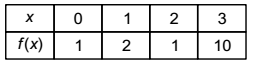
- The values of a function f(x) are tabulated below:

Using Newton's forward difference formula, the cubic polynomial that can be fitted to the above data, is
-
View Hint View Answer Discuss in Forum
Difference table as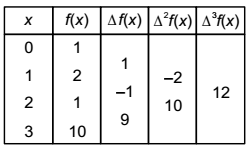
We take x0 = 0, p = x - 0 = x [∵ k = 1] k
using Newton’s forward interpolation formulae, we getf(x) = f(0) + x Δ f(0) + x(x-1) 1 1.2
∆²f(0) + x(x-1)(x-2) ∆3f(0) 1.2.3 = 1 + x(1) + x(x-1) (-2) + x(x-1)(x-2) (12) 2 6
= 1 + x + (x – x²) + 2x(x² – 3x + 2)
= 1 + x + x – x² + 2x3 – 6x + 4x
= 2x3 – 7x² + 6x + 1Correct Option: D

Difference table as
We take x0 = 0, p = x - 0 = x [∵ k = 1] k
using Newton’s forward interpolation formulae, we getf(x) = f(0) + x Δ f(0) + x(x-1) 1 1.2
∆²f(0) + x(x-1)(x-2) ∆3f(0) 1.2.3 = 1 + x(1) + x(x-1) (-2) + x(x-1)(x-2) (12) 2 6
= 1 + x + (x – x²) + 2x(x² – 3x + 2)
= 1 + x + x – x² + 2x3 – 6x + 4x
= 2x3 – 7x² + 6x + 1
- A box contains 4 red balls and 6 black balls. Three balls are selected randomly from the box one after another, without replacement. The probability that the selected set contains one, red ball and two black balls is
-
View Hint View Answer Discuss in Forum
Given : Red Black 4 6
Selection will be RBB or BBR of BRBProbability of selecting RBB = 4 × 6 × 5 10 9 8 Probability of selecting BBR = 6 × 5 × 4 10 9 8
Probability of selecting BRB = 6 × 4 × 5 10 9 8
P (Red = 1) = sum of above three probabilities = 0.5Correct Option: D
Given : Red Black 4 6
Selection will be RBB or BBR of BRBProbability of selecting RBB = 4 × 6 × 5 10 9 8 Probability of selecting BBR = 6 × 5 × 4 10 9 8
Probability of selecting BRB = 6 × 4 × 5 10 9 8
P (Red = 1) = sum of above three probabilities = 0.5
- A box contains 2 washers, 3 nuts and 4 bolts. Items are drawn from the box at random one at a time without replacement. The probability of drawing 2 washers first followed by 3 nuts and subsequently the 4 bolts is
-
View Hint View Answer Discuss in Forum
Given: Washers – 2, Nuts – 3, Bolts – 4,
Total– 9 objects
Hence probability of drawing two washers from 9 objects= 2C2 = 1 9C2 36
Probability of drawing, 3 nuts out of remaining 7 objects is= 4C4 = 1 4C4
Probability of drawing 4 bolts out of remaining 4 bolts∴ Required Probability = 1 × 1 × 1 = 1 36 35 1260
Correct Option: C
Given: Washers – 2, Nuts – 3, Bolts – 4,
Total– 9 objects
Hence probability of drawing two washers from 9 objects= 2C2 = 1 9C2 36
Probability of drawing, 3 nuts out of remaining 7 objects is= 4C4 = 1 4C4
Probability of drawing 4 bolts out of remaining 4 bolts∴ Required Probability = 1 × 1 × 1 = 1 36 35 1260
- If three coins are tossed simultaneously, the probability of getting at least one head is
-
View Hint View Answer Discuss in Forum
Let probability of getting atleast one head = P(H) then P(at least one head) = 1 – P (no head)
⇒ P(H) = 1– P(all tails)
But in all cases, 23 = 8∴ P(H) = 1 - 1 = 7 8 8
Alternately: Probability of getting at least one head
Correct Option: D
Let probability of getting atleast one head = P(H) then P(at least one head) = 1 – P (no head)
⇒ P(H) = 1– P(all tails)
But in all cases, 23 = 8∴ P(H) = 1 - 1 = 7 8 8
Alternately: Probability of getting at least one head

