76. A box contains 5 black and 5 red balls. Two balls are randomly picked one after another from the box, without replacement. The probability for both balls being red is

1. 1. 1

      90

   
   
   

   2. 1

      2

   
   
   

   3. 19

      90

   
   
   

   4. 2

      9

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   The probability of drawing a red ball =	5
   	10

   
   

   If the ball is not replaced, the box will have a ball, so probability of drawing the red ball in next chance =	4
   	9

   
   Hence probability of drawing 2 balls
   

   =		5	×	4	=	2
   		10		9		9

   
   

   Correct Option: D

   The probability of drawing a red ball =	5
   	10

   
   

   If the ball is not replaced, the box will have a ball, so probability of drawing the red ball in next chance =	4
   	9

   
   Hence probability of drawing 2 balls
   

   =		5	×	4	=	2
   		10		9		9

   
   

---

77. Given two complex numbers Z1 = 5 + (5√3)i and Z2 =	2	+ 2i the arguement of	Z1	in degree is
    	√3		Z2

1. 1. 0

   
   
   

   2. 30

   
   
   

   3. 60

   
   
   

   4. 90

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

   Correct Option: A

   
   

---

---

78. The product of two complex numbers (1+ i) and 2 – 5i is

1. 1. 7 – 3i

   
   
   

   2. 3 – 4i

   
   
   

   3. –3 – 4i

   
   
   

   4. 7 + 3i

   
   
   

---

1. View Hint View Answer Discuss in Forum

   (1 + i) (2 – 5i) = 2 – 5i + 2i + 5
   = 7 – 3i

   Correct Option: A

   (1 + i) (2 – 5i) = 2 – 5i + 2i + 5
   = 7 – 3i

---

79. The modulus of the complex number		3 + 4i		is
    		1 - 2i

1. 1. 5

   
   
   

   2. √5

   
   
   

   3. 1 / √5

   
   
   

   4. 1 / 5

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given : z =	3 + 4i
   	1 - 2i

   
   Rationalizing the denominator, we get
   

   z =	3+4i	×	1+2i
   	1-2i		1+2i

   
   

   =	3 + 6i + 4i - 8
   	5

   
   

   =	10i - 5	= 2i - 1
   	5

   
   ∴ Modulus of |z| = |2i - 1| √2² + (-1)² = √5
   

   Correct Option: B

   Given : z =	3 + 4i
   	1 - 2i

   
   Rationalizing the denominator, we get
   

   z =	3+4i	×	1+2i
   	1-2i		1+2i

   
   

   =	3 + 6i + 4i - 8
   	5

   
   

   =	10i - 5	= 2i - 1
   	5

   
   ∴ Modulus of |z| = |2i - 1| √2² + (-1)² = √5
   

---

---

80. The argument of the complex number {(1 + i) / (1 - i)} , where i = √-1 is

1. 1. -π

   
   
   

   2. -π / 2

   
   
   

   3. π / 2

   
   
   

   4. π

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

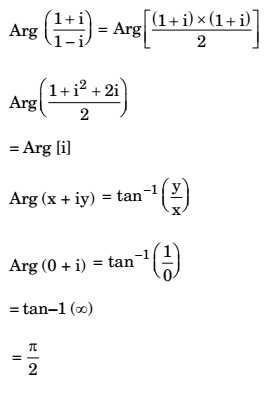
   Correct Option: C

   
   

---