Programming and data structure miscellaneous
- How many distinct binary search trees can be created out of 4 distinct keys?
-
View Hint View Answer Discuss in Forum
The number of keys as per given are 4
Applying the direct formula Bn = 1 / (n + 1) × (2n! / n!n!)
where, Bn is number of binary trees and n is the number of keys.
→ Bn = 1/(4 + 1) × (8!/ 4!4!)
→ Bn = 1/5 × (8 × 7 × 6 × 5 × 4!)/ 4!4!
→ Bn = 8 × 7 × 6/(4 × 3 × 2)
→ Bn = 56/4
→ Bn = 14
The total number of binary trees with n = 4 is 14.Correct Option: B
The number of keys as per given are 4
Applying the direct formula Bn = 1 / (n + 1) × (2n! / n!n!)
where, Bn is number of binary trees and n is the number of keys.
→ Bn = 1/(4 + 1) × (8!/ 4!4!)
→ Bn = 1/5 × (8 × 7 × 6 × 5 × 4!)/ 4!4!
→ Bn = 8 × 7 × 6/(4 × 3 × 2)
→ Bn = 56/4
→ Bn = 14
The total number of binary trees with n = 4 is 14.
- Postorder traversal of a given binary search tree, T produces the following sequence of keys 10, 9, 23, 22, 27, 25, 15, 50, 95, 60, 40, 29 Which one of the following sequences of keys can be the result of an in-order traversal of the tree T ?
-
View Hint View Answer Discuss in Forum
Inorder traversal of a BST always gives elements in increasing order. Among all four options, (a) is the only increasing order sequence.
Correct Option: A
Inorder traversal of a BST always gives elements in increasing order. Among all four options, (a) is the only increasing order sequence.
- The inorder and preorder traversal of a binary tree are d b e a f c g and a b d e c f g, respectively The postorder traversal of the binary tree is
-
View Hint View Answer Discuss in Forum
The inorder traversal sequence is dbeafcg and the preorder traversal sequence is abdecfg so, the tree is

In the postorder traversal, the sequence is debfgca.Correct Option: A
The inorder traversal sequence is dbeafcg and the preorder traversal sequence is abdecfg so, the tree is

In the postorder traversal, the sequence is debfgca.
- Consider the following C program segment where CellNode represents a node in a binary tree :
struct Cell Node {
struct Cell Node *leftChild;
int element; struct CellNode *rightChild;
}
int GetValue (struct CellNode *ptr) {
int value = 0
if (ptr! = NULL)
if ((ptr - > leftChild = = NULL) &&
(ptr -> rightChild == NULL) {
value = 1;
else
value = value + GetValue (ptr -> leftChild)
+ GetValue (ptr -> rightChild);
}
return (value);
}
The value returned by GetValue when a pointer to the root of a binary tree is passed as its argument is
-
View Hint View Answer Discuss in Forum
A node is a leaf node if both left and right child nodes of it are NULL.
1) If node is NULL then return 0.
2) Else If left and right child nodes are NULL return 1.
3) Else recursively calculate leaf count of the tree using below formula.
Leaf count of a tree = Leaf count of left subtree + Leaf count of right subtree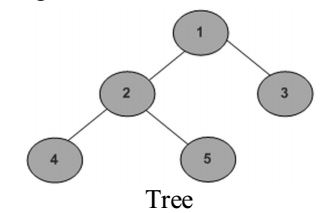
Leaf count for the above tree is 3.Correct Option: C
A node is a leaf node if both left and right child nodes of it are NULL.
1) If node is NULL then return 0.
2) Else If left and right child nodes are NULL return 1.
3) Else recursively calculate leaf count of the tree using below formula.
Leaf count of a tree = Leaf count of left subtree + Leaf count of right subtree
Leaf count for the above tree is 3.
- The inorder and preorder traversal of a binary tree are d b e a f c g and a b d e c f g, respectively The postorder traversal of the binary tree is.
-
View Hint View Answer Discuss in Forum
In order d b e a f c g
preorder a b d e c f g
1st element of pre order is root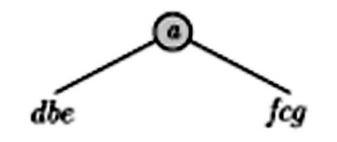
in preorder b is before d e. & c is before f g.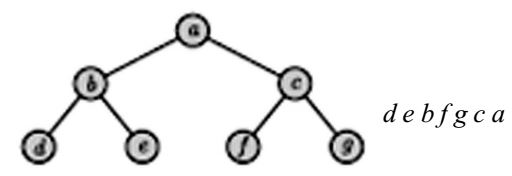
Correct Option: A
In order d b e a f c g
preorder a b d e c f g
1st element of pre order is root
in preorder b is before d e. & c is before f g.

