Programming and data structure miscellaneous
- Consider a rooted n node binary tree represented using pointers. The best upper bound on the time required to determine the number of subtrees having exactly 4 nodes is O (na logbn). Then the value of a + 10b is ______.
-
View Hint View Answer Discuss in Forum
1 to 1
Value of a + 10b = 1.
We can find the subtree with 4 nodes in O(n) time, we can use following Algorithm :
(1) Transverse the tree in bottom up manner and find size of subtree rooted with current node.
(2) If size becomes 4, then print the current node. int print 4 subtree (struct Node *root)
{
if (root = = NULL)
return 0;
int l = print 4 subtree (root → left);
int r = print 4 subtree (root → right);
if ((l + r + 1) = = 4)
printf (“%d”, root ® data);
return (l + r + 1)
}Correct Option: C
1 to 1
Value of a + 10b = 1.
We can find the subtree with 4 nodes in O(n) time, we can use following Algorithm :
(1) Transverse the tree in bottom up manner and find size of subtree rooted with current node.
(2) If size becomes 4, then print the current node. int print 4 subtree (struct Node *root)
{
if (root = = NULL)
return 0;
int l = print 4 subtree (root → left);
int r = print 4 subtree (root → right);
if ((l + r + 1) = = 4)
printf (“%d”, root ® data);
return (l + r + 1)
}
- Consider a B+ tree in which the search key is 12 bytes long, block size is 1024 bytes, record pointer is 10 bytes long and block pointer is 8 bytes long. The maximum number of keys that can be accommodated in each non – leaf node of the tree is ______.
-
View Hint View Answer Discuss in Forum
Suppose that ‘k’ is order of the non-leaf node k(8) + (k – 1)12 ≤ 1024
20k ≤ 1036k ≤ 
1036 
⇒ k ≤ 51 20
As the order is 51, maximum we can store 50 keys.Correct Option: D
Suppose that ‘k’ is order of the non-leaf node k(8) + (k – 1)12 ≤ 1024
20k ≤ 1036k ≤ 
1036 
⇒ k ≤ 51 20
As the order is 51, maximum we can store 50 keys.
- If the following system has non – trivial solution
px +qy + rz = 0
qx + ry + pz = 0
rx + py +qz = 0
then which one of the following options is TRUE ?
-
View Hint View Answer Discuss in Forum
For non-trivial solution, we have | A | = 0
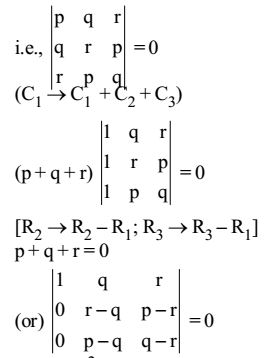
⇒ (r – q)2 – (p – q) (p – r) = 0
⇒ p2 + q2 + r2 – pq – qr – pr = 0
⇒ (p – q)2 + (q – r)2 + (r – p)2 = 0
⇒ p – q = 0; q – r = 0, r – p = 0
⇒ p = q = r.Correct Option: C
For non-trivial solution, we have | A | = 0
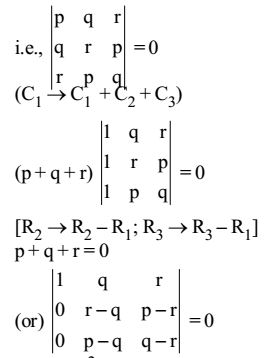
⇒ (r – q)2 – (p – q) (p – r) = 0
⇒ p2 + q2 + r2 – pq – qr – pr = 0
⇒ (p – q)2 + (q – r)2 + (r – p)2 = 0
⇒ p – q = 0; q – r = 0, r – p = 0
⇒ p = q = r.
- Consider a binary tree T that has 200 leaf nodes. Then, the number of nodes in T that have exactly two children are _______.
-
View Hint View Answer Discuss in Forum
Let the number of leaf nodes of a binary tree with ‘n’ vertices be ‘p’ then the tree has
(i) ‘p’ vertices of degree ‘1’
(ii) one vertex (i.e. root of T) of degree ‘2’.
(iii) 'n – p – 1' vertices of degree ‘3’
(iv) 'n –1' edges
∴ By Handshaking theorem, p × 1 + 1 × 2 + (n – p –1)×3 = 2(n –1)
⇒ n = 2 p – 1
= 399 as p = 200
∴ Number of nodes having exactly two children are n – p i.e., 199Correct Option: A
Let the number of leaf nodes of a binary tree with ‘n’ vertices be ‘p’ then the tree has
(i) ‘p’ vertices of degree ‘1’
(ii) one vertex (i.e. root of T) of degree ‘2’.
(iii) 'n – p – 1' vertices of degree ‘3’
(iv) 'n –1' edges
∴ By Handshaking theorem, p × 1 + 1 × 2 + (n – p –1)×3 = 2(n –1)
⇒ n = 2 p – 1
= 399 as p = 200
∴ Number of nodes having exactly two children are n – p i.e., 199
- While inserting the elements 71, 65, 84, 69, 67, 83 in an empty Binary Search Tree (BST) in the sequence shown, the element in the lowest level is
-
View Hint View Answer Discuss in Forum
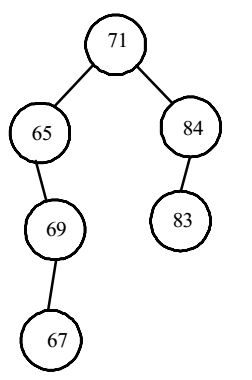
Correct Option: B


