Programming and data structure miscellaneous
- Let T be a binary search tree with 15 nodes. The minimum and maximum possible heights of T are :
Note : The height of a tree with a single node is 0.
-
View Hint View Answer Discuss in Forum
Since there are 15 nodes, hence the minimum height of the tree will be 3 (when tree will be balanced).

Min. height = floor (log2 N)
= floor (log2 15) = 3
The maximum height will be when the tree is skew tree, which will give rise to height 14 either it will be left or right skewed tree. Hence option (b) is correct.Correct Option: B
Since there are 15 nodes, hence the minimum height of the tree will be 3 (when tree will be balanced).

Min. height = floor (log2 N)
= floor (log2 15) = 3
The maximum height will be when the tree is skew tree, which will give rise to height 14 either it will be left or right skewed tree. Hence option (b) is correct.
- (a) Suppose you are given an empty B+-tree where each node (leaf and internal) can store up to 5 key values. Suppose values 1, 2,... 10 are inserted, in order, into the tree, show the tree pictorially
(i) After 6 insertions, and
(ii) After all 10 insertions
Do NOT show intermediate stages.
(b) Suppose instead of splitting a node when it is full, we try to move a value to the left sibling. If there is no left sibling, or the left sibling is full, we split the node. Show the tree after values, 1, 2,..., 9 have been inserted. Assume, as in (a) that each node can hold up to 5 keys.
(c) In general, suppose a B+-tree node can hold a maximum of m keys, and you insert a long sequence of keys in increasing order. Then what approximately is the average number of keys in each leaf level node.
(i) In the normal case, and
(ii) with the insertion as in (b).
-
View Hint View Answer Discuss in Forum
(a)
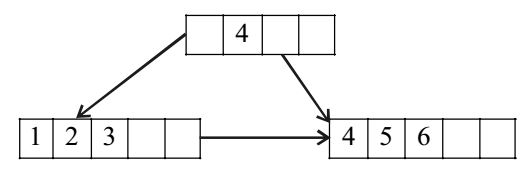
(b)
(c)(i) 
m 
or m 2 2
(ii) mCorrect Option: D
(a)

(b)
(c)(i) 
m 
or m 2 2
(ii) m
- The number of leaf nodes in a rooted tree of n nodes, with each node having 0 or 3 children is
-
View Hint View Answer Discuss in Forum
Consider following rooted trees

n = 4
(2n + 1)/3 = 3
No. of leaf nodes = 3
Hence (d) is correct option.Correct Option: D
Consider following rooted trees

n = 4
(2n + 1)/3 = 3
No. of leaf nodes = 3
Hence (d) is correct option.
- Consider the following C program segment
struct Cell Node {
struct Cell Node *left Child;
int element;
struct Cell Node *right Child;
}
int Dosomething (struct Cell Node *ptr)
{
int value = 0;
if (ptr! = NULL)
{ if (ptr-> left Child! = NULL)
value = 1 + Dosomething (ptr -> left Child);
if(ptr-> rightChild! = NULL)
value = max (value, 1 + Dosomething (ptr- > rightChild));
}
return (value);
}
The value returned by the function Dosomething when a pointer to the root of a non-empty tree is passed as argument is
-
View Hint View Answer Discuss in Forum
Value initialized by 0. If any root node has left child then it adds 1 to the value & move to left child & if any mode has right child also then also calculated the value using recursion & take maximum of both left & right value is taken.
So we know that height is the largest distance between root node & leaf. Therefore, this program calculates heights.
Hence (d) is correct option.Correct Option: D
Value initialized by 0. If any root node has left child then it adds 1 to the value & move to left child & if any mode has right child also then also calculated the value using recursion & take maximum of both left & right value is taken.
So we know that height is the largest distance between root node & leaf. Therefore, this program calculates heights.
Hence (d) is correct option.
- Assume that the operators +, –, ×, are left associative and ^ is right associative. The order of precedence (from highest to lowest) is ^, ×, +, –. The postfix expression corresponding to the infix expression a + b × c – d ^ e ^ f is
-
View Hint View Answer Discuss in Forum
a + b × c – d ^ e ^ f
a + b × c – d ^ e f ^
a + b × c – d e f ^ ^
a + b c × – d e f ^ ^
a b c × – d e f ^ ^
a b c × + d e f ^ ^
a b c × + d e f ^ ^–
the result is obtained.Correct Option: A
a + b × c – d ^ e ^ f
a + b × c – d ^ e f ^
a + b × c – d e f ^ ^
a + b c × – d e f ^ ^
a b c × – d e f ^ ^
a b c × + d e f ^ ^
a b c × + d e f ^ ^–
the result is obtained.

