Programming and data structure miscellaneous

Programming and data structure miscellaneous

Easy Questions

Programming & Data Structure

Programming and data structure miscellaneous
  1. A binary tree T has 20 leaves. The number of nodes in T having two children is _____.








  1. View Hint View Answer Discuss in Forum

    Let the number of vertices of a binary tree with ‘p’ leaves be n then the tree has–
    (i) p vertices (i.e., leaves) of degree 1
    (ii) one vertex (i.e.., root of T) of degree 2
    (iii) 'n - p -1' (i.e., interval) vertices of degree 3
    (iv) n -1edges
    ∴ By Handshaking theorem, p × 1 + 1 × 2 + (n – p – 1) × 3 = 2 (n – 1)
    ⇒ n = 2p – 1
    = 39 as p = 20
    ⇒ n – p =19 vertices have exactly two children

    Correct Option: B

    Let the number of vertices of a binary tree with ‘p’ leaves be n then the tree has–
    (i) p vertices (i.e., leaves) of degree 1
    (ii) one vertex (i.e.., root of T) of degree 2
    (iii) 'n - p -1' (i.e., interval) vertices of degree 3
    (iv) n -1edges
    ∴ By Handshaking theorem, p × 1 + 1 × 2 + (n – p – 1) × 3 = 2 (n – 1)
    ⇒ n = 2p – 1
    = 39 as p = 20
    ⇒ n – p =19 vertices have exactly two children

  1. Consider a complete binary tree where the left and the right subtrees of the root are max-heaps. The lower bound for the number operations to convert the tree to a heap is








  1. View Hint View Answer Discuss in Forum

    NA

    Correct Option: A

    NA

  1. With reference to the B+ tree index of order 1 shown below, the minimum number of nodes (including the Root node) that must be fetched in order to satisfy the following query: "Get all records a search key greater than or equal to 7 and less than 15" is ____.








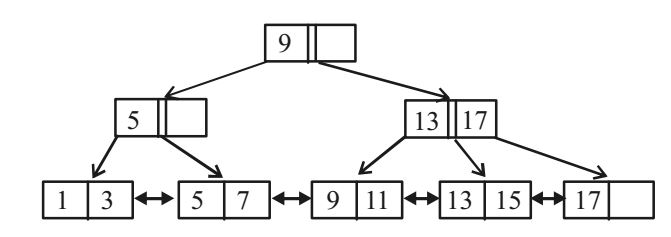
  1. View Hint View Answer Discuss in Forum

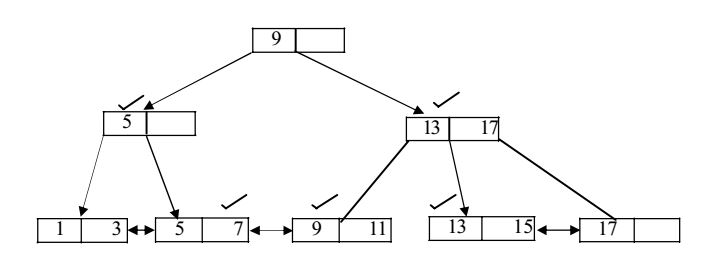
    Correct Option: C

  1. Which of the following is/are correct inorder traversal sequence(s) of binary search tree(s) ?
    I. 3, 5, 7, 8, 15, 19, 25 II. 5, 8, 9, 12, 10, 15, 25
    III. 2, 7, 10, 8, 14, 16, 20 IV. 4, 6, 7, 9, 18, 20, 25








  1. View Hint View Answer Discuss in Forum

    In-order traversal of binary search tree gives ascending orders and in BST, at every node root element is greater than and equal to all element present in left sub-tree and less than or equal to all the elements in right subtree.

    Correct Option: A

    In-order traversal of binary search tree gives ascending orders and in BST, at every node root element is greater than and equal to all element present in left sub-tree and less than or equal to all the elements in right subtree.

  1. The height of a tree is the length of the longest root-to-leaf path in it. The maximum and minimum number of nodes in a binary tree of height 5 are








  1. View Hint View Answer Discuss in Forum

    We know that the maximum no. of nodes in a binary tree with (height) h = 2h + 1 – 1.
    Here h = 5, then, we easily calculate the h as :
    h = 25 + 1 – 1= 64 – 1 = 63
    And the minimum no. of nodes with height h is h + 1.
    ∴ h = 5

    Correct Option: A

    We know that the maximum no. of nodes in a binary tree with (height) h = 2h + 1 – 1.
    Here h = 5, then, we easily calculate the h as :
    h = 25 + 1 – 1= 64 – 1 = 63
    And the minimum no. of nodes with height h is h + 1.
    ∴ h = 5