Programming and data structure miscellaneous
Direction: The subset - sum problem is defined as follows : Given a set of n positive integers, S = {a1, a2, a3, ...an}, and positive integer W, is there a subset of S whose elements sum to W? A dynamic program for solving this problem uses a 2- dimensional Boolean array, X, with n rows and W + 1 columns. X[i, j], 1 ≤ i ≤ n,0 ≤ j ≤ W, is true if and only if there is a subset of {a1, a2, ....ai} whose elements sum to j
- Which entry of the array X, if true, implies that there is a subset whose elements sum to W?
-
View Hint View Answer Discuss in Forum
The algorithm of dynamic programming has n rows & w columns.These would be filled dynamically depending upon previous rows &columns. So X[n,w] will be filled in the last & this would give the result. If X[n,w] = 1 i.e. TRUE, then we know that there is subset present whose sum = integer w. Otherwise subset not present.
Hence (c) is correct option.Correct Option: C
The algorithm of dynamic programming has n rows & w columns.These would be filled dynamically depending upon previous rows &columns. So X[n,w] will be filled in the last & this would give the result. If X[n,w] = 1 i.e. TRUE, then we know that there is subset present whose sum = integer w. Otherwise subset not present.
Hence (c) is correct option.
- Which of the following is valid for 2 ≤ i ≤ n and ai ≤ j ≤ W ?
-
View Hint View Answer Discuss in Forum
Dynamic programming can be successfully used, i.e n rows for n elements &w + 1 columns.
Each row is filled on the basis of its previous rows & the (j – ai) – th column.
If any of them is 0 then X[i, j] should be zero. This require X[i, j] = X[i – 1, j] ∨ × [i – 1, j – ai]
Hence (b) is correct option.Correct Option: B
Dynamic programming can be successfully used, i.e n rows for n elements &w + 1 columns.
Each row is filled on the basis of its previous rows & the (j – ai) – th column.
If any of them is 0 then X[i, j] should be zero. This require X[i, j] = X[i – 1, j] ∨ × [i – 1, j – ai]
Hence (b) is correct option.
Direction: The procedure given below is required to find and replace certain characters inside an input character string supplied in array A. The characters to be replaced are supplied in array oldc, while their respective replacement characters are supplied in array newc. Array A has a fixed length of five characters, while arrays oldc and newc contain three characters each. However, the procedure is flawed.
void find_and_replace (char *A, char *oldc, char *newc)
{
for (int i=0; i<5; i++)
for (int j=0; j<3; j++)
if (A[i]==oldc[j]) A[i] = newc[j];
}
The procedure is tested with the following four test cases.
1. oldc = “abc”, newc = “da b”
2. oldc = “cde”, newc = “bcd”
3. oldc = “bca”, newc = “cda”
4. oldc = “abc”, newc = “bac”
- If array A is made to hold the string “abcde”, which of the above four test cases will be successful in exposing the flaw in this procedure?
-
View Hint View Answer Discuss in Forum
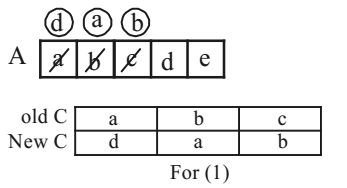
Here, when the element of array A and old C match, we replace that array element of A with array element of new C for every element of A array update occurs maximum one time. Similarly for (2) array element of A has updated with array element of new C less than or equal to one time.
Now, for (3), when i = O, value of A which old C[2] i.e. ‘a’ and replace with new C[2] i.e. also ‘a’, So, no changes. when i = 1 value of array. A[1] = ‘b’
Match with Old C [O] = ‘b’ and replace with new C [O] = ‘C’.
Now, A [1] = ‘C’, which equal with ‘d’. Next element of old C [1] = ‘C’.
So, replace again with new C [1] = ‘d’.
Now, we can say here in Array A [1] value replace with new C [O] value, and that new C [O] value replace with next new C [1] value.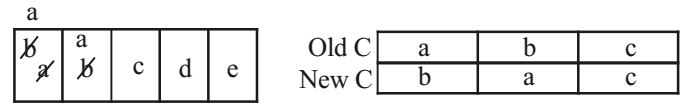
Similarly for (4) here 2 times replacement for A[O] with element new C [O] and new C [1]. Updating of new C value with another new C value is calling flow here, Hence the option (c) is correct.Correct Option: B

Here, when the element of array A and old C match, we replace that array element of A with array element of new C for every element of A array update occurs maximum one time. Similarly for (2) array element of A has updated with array element of new C less than or equal to one time.
Now, for (3), when i = O, value of A which old C[2] i.e. ‘a’ and replace with new C[2] i.e. also ‘a’, So, no changes. when i = 1 value of array. A[1] = ‘b’
Match with Old C [O] = ‘b’ and replace with new C [O] = ‘C’.
Now, A [1] = ‘C’, which equal with ‘d’. Next element of old C [1] = ‘C’.
So, replace again with new C [1] = ‘d’.
Now, we can say here in Array A [1] value replace with new C [O] value, and that new C [O] value replace with next new C [1] value.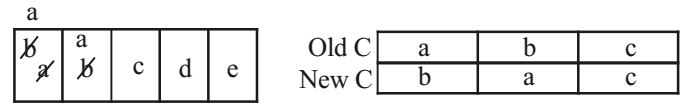
Similarly for (4) here 2 times replacement for A[O] with element new C [O] and new C [1]. Updating of new C value with another new C value is calling flow here, Hence the option (c) is correct.
- The tester now tests the program on all input strings of length five consisting of characters ‘a’, ‘b’, ‘c’, ‘d’ and ‘e’ with duplicates allowed. If the tester carries out this testing with the four test cases given above, how many test cases will be able to capture the flaw?
-
View Hint View Answer Discuss in Forum
Analyzing the flow in the function. Fix an 'i' in the outer loop.
Suppose A[i] = old c[0], then A[i] is set to new c[0] [j = 0].
Now suppose that old c[1]= new c[0]
⇒ A[i] = old c[1] (after the j = 0th iteration)
which means in the next iteration with j = 1; A[i] again gets changed form new c[0] (or old c[1]) to new c[1] which is incorrect.
The current loop should "break" after a match is found and A[i] is replaced.
The inner loop should look like
for (int j = 0; j < 3, j + +)
if (A [i] = = old c[j])
A[j] = new c [j];
break;
The above flow is exposed by the test cases 3 & 4 only. For test 1 and test 2, the expected output is produced by the code. Test 3 Expected A after replacements
= "abcde" → "acdde"
result from code = "abcde" → "addde"
Test 4 Expected "abcde" → "bacde"
result form code "abcde" → "abcde".
∴ Answer is 3 and 4 only (c)Correct Option: C
Analyzing the flow in the function. Fix an 'i' in the outer loop.
Suppose A[i] = old c[0], then A[i] is set to new c[0] [j = 0].
Now suppose that old c[1]= new c[0]
⇒ A[i] = old c[1] (after the j = 0th iteration)
which means in the next iteration with j = 1; A[i] again gets changed form new c[0] (or old c[1]) to new c[1] which is incorrect.
The current loop should "break" after a match is found and A[i] is replaced.
The inner loop should look like
for (int j = 0; j < 3, j + +)
if (A [i] = = old c[j])
A[j] = new c [j];
break;
The above flow is exposed by the test cases 3 & 4 only. For test 1 and test 2, the expected output is produced by the code. Test 3 Expected A after replacements
= "abcde" → "acdde"
result from code = "abcde" → "addde"
Test 4 Expected "abcde" → "bacde"
result form code "abcde" → "abcde".
∴ Answer is 3 and 4 only (c)
- Let A be a square matrix of size n × n. Consider the following pseudocode. What is the expected output?
c = 100;
for i = 1 to n do for j = 1 to n do
{
Temp = A [i] [j] + C;
A [i] [j] = A [j] [i];
A [j] [i] = Temp – C;
}
for i = 1 to n do
for j = 1 to n do
output (A [i] [j]);
-
View Hint View Answer Discuss in Forum
For the given pseudo code, each element of the upper triangle is interchanged by the corresponding element in lower triangle and later the lower triangular element is interchanged by the upper triangular once. Thus the final output matrix will be same as that of input matrix A.
Correct Option: A
For the given pseudo code, each element of the upper triangle is interchanged by the corresponding element in lower triangle and later the lower triangular element is interchanged by the upper triangular once. Thus the final output matrix will be same as that of input matrix A.

