Programming and data structure miscellaneous
- A queue is implemented using an array such that ENQUEUE and DEQUEUE operations are performed efficiently. Which one of the following statements is CORRECT (n refers to the number of items in the queue)?
-
View Hint View Answer Discuss in Forum
We can use circular array to implement both O(1) time.
Correct Option: A
We can use circular array to implement both O(1) time.
- A circular queue has been implemented using a singly linked list where each node consists of a value and a single pointer pointing to the next node. We maintain exactly two external pointers FRONT and REAR pointing to the front node and the rear node of the queue, respectively. Which of the following statements is/are CORRECT for such a circular queue, so that insertion and deletion operations can be performed in 0 (1) time?
I. Next pointer of front node points to the rear node.
II. Next pointer of rear node points to the front node.
-
View Hint View Answer Discuss in Forum
In circular queue next pointer of Rear node pointing to the Front Node will lead to insertion in a queue is always from REAR and deletion is always from FRONT node in Θ(1) time.
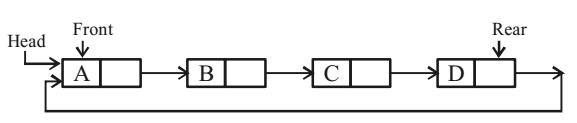
Hence, option (B) is correct.Correct Option: B
In circular queue next pointer of Rear node pointing to the Front Node will lead to insertion in a queue is always from REAR and deletion is always from FRONT node in Θ(1) time.

Hence, option (B) is correct.
- What is the minimum number of stacks of size n required to implement a queue of size n ?
-
View Hint View Answer Discuss in Forum
2 stacks. You can even simulate a queue using only one stack. The second (temporary) stack can be simulated by the call stack of recursive calls to the insert method. The principle stays the same when inserting a new element into the queue:
⚈ You need to transfer elements from one stack to another temporary stack, to reverse their order. Then push the new element to be inserted, onto the temporary stack. Then transfer the elements back to the original stack.
⚈ The new element will be on the bottom of the stack, and the oldest element is on top (first to be popped).Correct Option: B
2 stacks. You can even simulate a queue using only one stack. The second (temporary) stack can be simulated by the call stack of recursive calls to the insert method. The principle stays the same when inserting a new element into the queue:
⚈ You need to transfer elements from one stack to another temporary stack, to reverse their order. Then push the new element to be inserted, onto the temporary stack. Then transfer the elements back to the original stack.
⚈ The new element will be on the bottom of the stack, and the oldest element is on top (first to be popped).
- To evaluate an expression without any embedded function calls
-
View Hint View Answer Discuss in Forum
A stack machine implements registers with a stack. The operands of the arithmetic logic unit (ALU) are always the top two registers of the stack and the result from the ALU is stored in the top register of the stack. 'Stack machine' commonly refers to computers which use a Last-in, First-out stack to hold short-lived temporary values while executing individual program statements. The instruction set carries out most ALU actions with postfix (Reverse Polish notation) operations that work only on the expression stack, not on data registers or main memory cells. The same opcode that handles the frequent common case of an add, an indexed load, or a function call will also handle the general case involving complex subexpressions and nested calls
Correct Option: A
A stack machine implements registers with a stack. The operands of the arithmetic logic unit (ALU) are always the top two registers of the stack and the result from the ALU is stored in the top register of the stack. 'Stack machine' commonly refers to computers which use a Last-in, First-out stack to hold short-lived temporary values while executing individual program statements. The instruction set carries out most ALU actions with postfix (Reverse Polish notation) operations that work only on the expression stack, not on data registers or main memory cells. The same opcode that handles the frequent common case of an add, an indexed load, or a function call will also handle the general case involving complex subexpressions and nested calls
- Let S be a stack of size n ≥ 1. Starting with the empty stack, suppose we push the first n natural numbers in sequence, and then perform n pop operations. Assume that Push and Pop operations take X seconds each, and Y seconds elapse between the end of one such stack operations and the start of the next operation. For m ≥ 1, define the stack – life of m as the time elapsed from the end of Push (m) to the start of the pop operation that removes m from S. The average stack – life of an element of this stack is
-
View Hint View Answer Discuss in Forum
Let us represent stack-life, of ith element as s(i). The ith element will be in stack till (n–i) elements are
pushed and popped. Plus one more y for the time interval between the push of ith element and the (i+1)th element. So,
S(i) = y + 2(n–i). (y + x)
= y + 2(n – i). z
= y + 2nZ – 2iz
Where z = (y + x).Average, stack-file will, A = ∑ 
s(i) 
n
nA = ( ny + 2.n.n.z - 2.z.∑i )nA = ny + 2.n.n.z - 2.z. 
n(n + 1) 
2
n A = ny + 2. n.n.z – z (n.n) – n.z
A = y + 2 nz – (n + 1). z = y + (n–1). z
= y + (n – 1)(y + x) = n(x + y) – x.Correct Option: C
Let us represent stack-life, of ith element as s(i). The ith element will be in stack till (n–i) elements are
pushed and popped. Plus one more y for the time interval between the push of ith element and the (i+1)th element. So,
S(i) = y + 2(n–i). (y + x)
= y + 2(n – i). z
= y + 2nZ – 2iz
Where z = (y + x).Average, stack-file will, A = ∑ 
s(i) 
n
nA = ( ny + 2.n.n.z - 2.z.∑i )nA = ny + 2.n.n.z - 2.z. 
n(n + 1) 
2
n A = ny + 2. n.n.z – z (n.n) – n.z
A = y + 2 nz – (n + 1). z = y + (n–1). z
= y + (n – 1)(y + x) = n(x + y) – x.

