Programming and data structure miscellaneous

Programming and data structure miscellaneous

Easy Questions

Programming & Data Structure

Programming and data structure miscellaneous
  1. N items are stored in a sorted doubly linked list. For a delete operation, a pointer is provided to the record to be deleted. For a decrease-key operation, a pointer is provided to the record on which the operation is to be performed.
    An algorithm performs the following operations on the list in this order : Θ(N) delete, O(log N) insert, O(log N) find, and Θ(N) decrease-key. What is the time complexity of all these operations put together?








  1. View Hint View Answer Discuss in Forum

    The time complexity which can put all these operations together will be O(N2).

    Correct Option: C

    The time complexity which can put all these operations together will be O(N2).

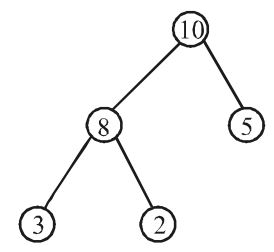
  1. A priority–queue is implemented as a max–heap. Initially, it has 5 elements. The level – order traversal of the heap is given below.
    10, 8, 5, 3, 2
    Two new elements 1 and 7 are inserted in the heap in that order. The level – order traversal of the heap after the insertion of the element is








  1. View Hint View Answer Discuss in Forum

    Initial level order traversal with 10, 8, 5, 3, 2

    Now, let us insert the values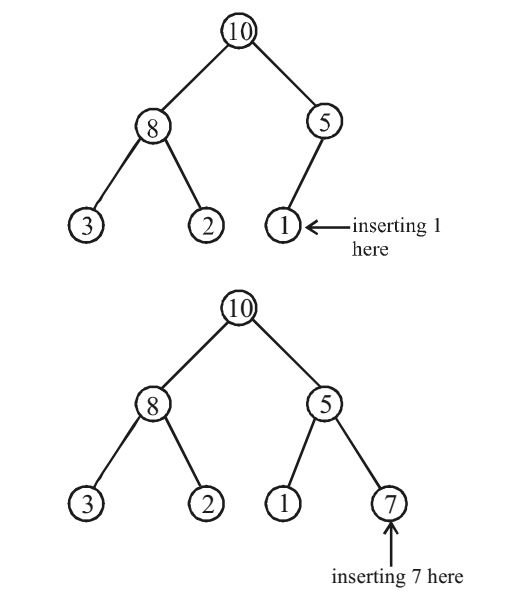


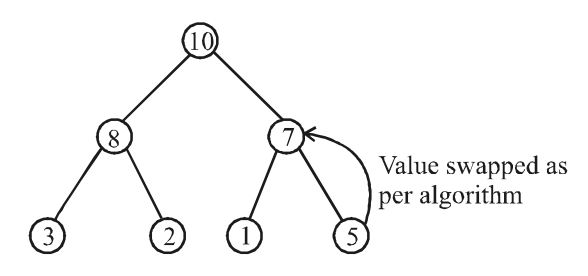
    Therefore, the level order traversal comes out to be 10, 8, 7, 3, 2, 1, 5

    Correct Option: D

    Initial level order traversal with 10, 8, 5, 3, 2

    Now, let us insert the values


    Therefore, the level order traversal comes out to be 10, 8, 7, 3, 2, 1, 5

  1. Suppose a circular queue of capacity (n – 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operations are carried out using REAR and FRONT as array index variables, respectively. Initially REAR = FRONT = 0. The conditions to detect queue full and queue empty are








  1. View Hint View Answer Discuss in Forum

    FRONT points to the first element that we can remove and then we increment FRONT REAR points to the first empty space in queue so we insert an element and increment REAR so now initially queue is empty F=R=0 insert A (AT 0th index) --> increment REAR (REAR =1 FRONT=0) now if we want to delete A we have FRONT pointing at that location so we delete A and increment FRONT (REAR=1 FRONT=1 queue empty).

    Correct Option: A

    FRONT points to the first element that we can remove and then we increment FRONT REAR points to the first empty space in queue so we insert an element and increment REAR so now initially queue is empty F=R=0 insert A (AT 0th index) --> increment REAR (REAR =1 FRONT=0) now if we want to delete A we have FRONT pointing at that location so we delete A and increment FRONT (REAR=1 FRONT=1 queue empty).

  1. Consider the following operation along the Enqueue and Dequeue operations on queues, where k is a global parameter. Multi-Dequeue(Q){ m = k while (Q is not empty) and (m > 0){ Dequeue(Q) m = m – 1 } } What is the worst case time complexity of a sequence of n queue operations on an initially empty queue ?








  1. View Hint View Answer Discuss in Forum

    To compute the worst case time complexity of a sequence of n queue operations on an initially empty queue is θ(n).
    Complexity of a squence of 'n' queue operations = Total complexity of Enqueue operations (α) + Total complexity of Dequeue operations (β).
    Total complexity of Dequeue operations (β) ≤ Total complexity of Enqueue operations
    β ≤ α ...(i)
    Total complexity of queue operations (α) ≤ n ...(ii)
    Total complexity of n operations = α + β
    ≤ α + α [From ...(i)]
    ≤ n + n [From... (ii)]
    ≤ 2 n
    ∴ Worst Case Time Complexity of 'n' operations is (a) θ(n).

    Correct Option: A

    To compute the worst case time complexity of a sequence of n queue operations on an initially empty queue is θ(n).
    Complexity of a squence of 'n' queue operations = Total complexity of Enqueue operations (α) + Total complexity of Dequeue operations (β).
    Total complexity of Dequeue operations (β) ≤ Total complexity of Enqueue operations
    β ≤ α ...(i)
    Total complexity of queue operations (α) ≤ n ...(ii)
    Total complexity of n operations = α + β
    ≤ α + α [From ...(i)]
    ≤ n + n [From... (ii)]
    ≤ 2 n
    ∴ Worst Case Time Complexity of 'n' operations is (a) θ(n).

  1. Let Q denote a queue containing sixteen numbers and S be an empty stack. Head (Q) returns the element at the head of the queue Q without removing it from Q. Similarly Top (S) returns the element at the top of S without removing it from S. Consider the algorithm given below.

    The maximum possible number of iterations of the while loop in the algorithm is _________.








  1. View Hint View Answer Discuss in Forum

    ∵ n = 16
    Therefore, maximum number of iterations will be n2 = 256

    Correct Option: C

    ∵ n = 16
    Therefore, maximum number of iterations will be n2 = 256