Programming and data structure miscellaneous

Programming and data structure miscellaneous

Easy Questions

Programming & Data Structure

Programming and data structure miscellaneous
  1. An operator delete (i) for a binary heap data structure is to be designed to delete the item in the i-th node. Assume that the heap is implemented in an array and i refers to the i-th index of the array. If the heap tree has depth d (number of edges on the path from the root to the farthest leaf), then what is the time complexity to re-fix the heap efficiently after the removal of the element ?








  1. View Hint View Answer Discuss in Forum

    NA

    Correct Option: B

    NA

  1. Consider the following nested representation of binary trees: (XYZ) indicates Y and Z are the left and right sub trees, respectively, of node X. Note that Y and Z may be NULL, or further nested. Which of the following represents a valid binary tree?








  1. View Hint View Answer Discuss in Forum

    (XYZ) indicates that Y is left sub-tree and Z is right subtree. Node is X

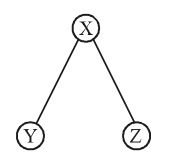
    As per given in the questions :
    (1 (234) (567))
    We get, the following tree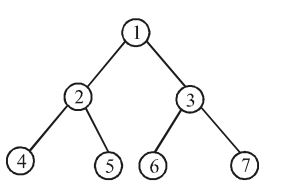

    1 is the root node
    2 and 3 are the non-leaf node
    4, 5, 6, 7 are the leaf node which may be null or further nested because in a binary tree every node has 0 or children and not just 1.

    Correct Option: C

    (XYZ) indicates that Y is left sub-tree and Z is right subtree. Node is X

    As per given in the questions :
    (1 (234) (567))
    We get, the following tree

    1 is the root node
    2 and 3 are the non-leaf node
    4, 5, 6, 7 are the leaf node which may be null or further nested because in a binary tree every node has 0 or children and not just 1.

  1. Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal. Respectively, of a complete binary tree. Which of the following is always true ?








  1. View Hint View Answer Discuss in Forum

    It is given that the given tree is complete binary tree. For a complete binary tree, the last visited node will always be same for inorder and preorder traversal. None of the above is true even for a complete binary tree. The option (a) is incorrect because the last node visited in Inorder traversal is right child and last node visited in Postorder traversal is root.
    The option (c) is incorrect because the last node visited in Preorder traversal is right child and last node visited in Postorder traversal is root.
    For option (b), see the following counter example.

    Inorder traversal is 4 2 5 1 6 3
    Preorder traversal is 1 2 4 5 3 6
    So, lastpost = 1, lastpre = 6, lastin = 3.
    Hence option (d) is correct.

    Correct Option: D

    It is given that the given tree is complete binary tree. For a complete binary tree, the last visited node will always be same for inorder and preorder traversal. None of the above is true even for a complete binary tree. The option (a) is incorrect because the last node visited in Inorder traversal is right child and last node visited in Postorder traversal is root.
    The option (c) is incorrect because the last node visited in Preorder traversal is right child and last node visited in Postorder traversal is root.
    For option (b), see the following counter example.

    Inorder traversal is 4 2 5 1 6 3
    Preorder traversal is 1 2 4 5 3 6
    So, lastpost = 1, lastpre = 6, lastin = 3.
    Hence option (d) is correct.

  1. A weight – balanced tree is a binary tree in which for each node, the number of nodes in the left sub tree is at least half and at most twice the number of nodes in the right sub tree. The maximum possible height (number of nodes on the path from the root to the furthest leaf) of such a tree on n nodes is best described by which of the following?








  1. View Hint View Answer Discuss in Forum

    Let the maximum possible height of a tree with n nodes is represented by H(n).
    The maximum possible value of H(n) can be approximately written using following recursion
    H(n) = H(2n/3) + 1
    The solution of above recurrence is log3/2 n. We can simply get it by drawing a recursion tree.

    Correct Option: D

    Let the maximum possible height of a tree with n nodes is represented by H(n).
    The maximum possible value of H(n) can be approximately written using following recursion
    H(n) = H(2n/3) + 1
    The solution of above recurrence is log3/2 n. We can simply get it by drawing a recursion tree.

  1. Consider the following 2 – 3 – 4 tree (i. e., B – tree with a minimum degree of two) in which each data item is a letter. The usual alphabetical ordering of letters is used in constructing the tree.

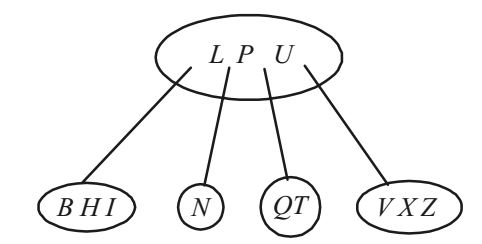
    What is the result of inserting G in the above tree?








  1. View Hint View Answer Discuss in Forum

    Since the given B tree is 2–3–4 tree, there can be at most 4 children or 3 keys. In B tree insertion, we start from root and traverse till the leaf node where key is to be inserted. While traversing. If we find a node which full, we split it. When we inseart G, we find root itself is full. So, we split it when we come down to left most leaf, we find that the leaf is also full, thus we split the leaf also. So, the percent node becomes H. L, P, U and select P as for splitting. Hence option (b) is correct.

    Correct Option: B

    Since the given B tree is 2–3–4 tree, there can be at most 4 children or 3 keys. In B tree insertion, we start from root and traverse till the leaf node where key is to be inserted. While traversing. If we find a node which full, we split it. When we inseart G, we find root itself is full. So, we split it when we come down to left most leaf, we find that the leaf is also full, thus we split the leaf also. So, the percent node becomes H. L, P, U and select P as for splitting. Hence option (b) is correct.